 设为首页
设为首页
 加入收藏
加入收藏
典型例题
填空题:
例 下列命题:①一组对边平行且相等的四边形是梯形;②一组对边平行且不相等的四边形是梯形;③一组对边平行,另一组对边相等的四边形是梯形;④一条直线与矩形的一组对边相交,必分矩形为两个直角梯形.其中真命题的序号是_______.
分析: 可采用反例法.即举的例子符合题没但不符合结论,从而说明原命题是假命题.①可举反例:平行四边形;②可证得另一组对边不平行,故符合定义;③可举反例:矩形;④直线与矩形垂直相交,则得到两个矩形.
答案 ②
说明:
梯形定义包括两个要素:1.一组对边平行;2.另一组对边不平行;不要认为只要有一组对边平行的四边形就是梯形.
阅读题:
例 (青海省2001年中考题)阅读了题和分析过程,并按要求进行证明.已知,四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,求证:四边形
,求证:四边形 ![]() 是等腰梯形.
是等腰梯形.
分析:要证四边形![]() 是等腰梯形,因为
是等腰梯形,因为![]() ,所以只要证四边形
,所以只要证四边形![]() 是梯形即可;又因为
是梯形即可;又因为![]() ,故只需证
,故只需证![]() 即可;要证
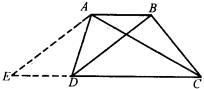
即可;要证![]() ,现有下图所示四种添作辅助线的方法,请任意选择其中两种图形,对原题进行证明.
,现有下图所示四种添作辅助线的方法,请任意选择其中两种图形,对原题进行证明.

解答略.
说明:这是一道设计得很好的阅读型试题.题目不仅给出了分析思路,还提供了四个已有辅助线的图形,说明本题有多种解法.但是,这些方法,体现了一个基本思路:努力转化,借助三角形知识加以突破,完成证明.
证明题:
例 如图,在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 为
为![]() 、
、![]() 的中点。
的中点。

求证:![]()
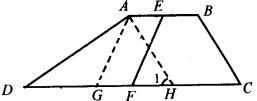
分析:梯形的问题往往转化成平行四边形或三角形来处理,根据条件来决定转化和辅助线的添加.
证法一:如图,延长![]() ,
,![]() 相交于
相交于![]() 点,连结
点,连结![]() ,
,![]() .
.
∵![]()
![]()
∵![]() 、
、![]() 为
为![]() 、
、![]() 的中点,∴
的中点,∴![]() ,
,![]()
∴![]() ,
,![]()

∵![]() ∴
∴![]() ∴
∴![]()
∴![]() 、
、![]() 、
、![]() 三点共线 ∴
三点共线 ∴![]() .
.
证法二 如图,过点![]() ,作
,作![]()

交![]() 于
于![]() ,
,![]() 交
交![]() 于
于![]()
∵![]() ,
,![]()
∴四边形![]() 是平行四边形
是平行四边形
∴![]()
同理:![]()
∵![]() ∴
∴![]()
∵![]()
∴![]()
∵![]() ∴
∴![]() ,
,![]()
∵![]() ∴
∴![]() ∴
∴![]()
∵![]() ∴
∴![]() 即
即![]()
证法三 如图,过点![]() 作
作![]() 交
交![]() 于
于![]() ,
,![]() 交
交![]() 于
于![]() .
.
∵![]() ,
,![]()
∴四边形![]() 是平行四边形
是平行四边形
∴![]()
同理:![]()
∴![]() ,
,
![]()
∵![]() ∴
∴![]()
∵![]() ∴
∴![]()
∵![]() ∴
∴![]() ∴
∴![]()
∴![]() ∴
∴![]() 即
即![]() .
.
说明:解题时要注意分析条件和结论,选择合适的切入点.
梯形典型例题之作图题
例 已知两底边及两条对角线求作梯形.
已知:线段![]() ,
,![]() ,
,![]() ,
,![]()
求作:梯形![]() ,使
,使![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
分析 如图,假设梯形![]() 已作出,
已作出,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,延长
,延长![]() 到
到![]() ,使
,使![]() ,连结
,连结![]() ,则四边形
,则四边形![]() 是平行四边形,所以
是平行四边形,所以![]() ,故先作
,故先作![]() .
.

作法(l)作![]() ,使
,使![]() ,
,![]() ,
,![]() .
.
(2)过点![]() 作
作![]() ,使
,使![]()
(3)在![]() 上截取
上截取![]() ,连结
,连结![]() ,
,![]()
∴ 四边形![]() 为所求作的梯形.
为所求作的梯形.
证明 ∵![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
∵ ![]() ∴四边形
∴四边形![]() 是平行四边形
是平行四边形
∴![]() ∴梯形
∴梯形![]() 就是所求作的梯形.
就是所求作的梯形.
讨论: 如果![]() ,
,![]() ,
,![]() 三条线段中,最长的一条线段大于或等于其他两条线段之和,则此作图题无解.
三条线段中,最长的一条线段大于或等于其他两条线段之和,则此作图题无解.
梯形典型例题之面积题
例 如图,在梯形![]() 中,
中,![]() ,
,![]() 为
为![]() 的中点.
的中点.
求证:![]() .
.

分析:梯形的问题往往转化成平行四边形或三角形来处理,根据条件来决定转化和辅助线的添加.
证法一 如图,延长![]() 交
交![]() 的延长线于
的延长线于![]() .
.
∵![]() ∴
∴![]() ,
,![]()
∵![]() ∴
∴![]()
![]()
![]()
∴![]() ,
,![]() ∴
∴![]() 是
是![]() 的中线
的中线
∴![]()
∴![]()
∴![]()

证法二 如图,过![]() 点作
点作![]() 交
交![]() 于
于![]() ,交
,交![]() 的延长线于
的延长线于![]() .
.

∵![]() ∴
∴![]()
∵![]() ∴
∴![]()
![]()
![]()
∴![]() ∴
∴ ![]()
∵ ![]() ∴
∴![]()
说明:解题时要注意分析条件和结论,选择合适的切入点.