 设为首页
设为首页
 加入收藏
加入收藏
关于椭圆最远点和最近点的证明
设 ![]() 是椭圆
是椭圆 ![]() 上的一点,
上的一点, ![]() 、
、 ![]() 分别是椭圆的左右焦点,求证:
分别是椭圆的左右焦点,求证: ![]() (
( ![]() 为椭圆的半焦距).
为椭圆的半焦距).
证明一:运用椭圆的定义及平面几何知识
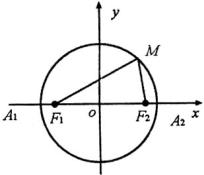 ∵
∵ ![]() ,
,
∴ ![]() . ①
. ①
又∵ ![]() ,
,
∴ ![]() .
.
即 ![]() .
.
由①式可得 ![]() ,
,
∴ ![]() .
.
当 ![]() 点在左端点
点在左端点 ![]() 上时,
上时, ![]() 是最大值;
是最大值;
当 ![]() 点在右端点
点在右端点 ![]() 上时,
上时, ![]() 是最小值.
是最小值.
证明二:应用椭圆的第二定义,设椭圆的离心率为 ![]() ,
, ![]() 则
则 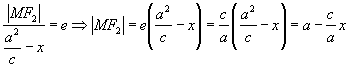 .
.
∵ ![]() .
.
∴当 ![]() 点在左端点
点在左端点 ![]() 上时,
上时, ![]() 是最大值;
是最大值;
当 ![]() 点在右端点
点在右端点 ![]() 上时,
上时, ![]() 是最小值.
是最小值.
证明三:应用椭圆的参数方程.
设 ![]() 的坐标为
的坐标为 ![]() ,则有
,则有 ![]() (
( ![]() 为参数).
为参数).
焦点 ![]() ,
,
![]()
![]()
![]() .
.
当 ![]() ,即
,即 ![]() 点在左端点
点在左端点 ![]() 上时,
上时, ![]() 是最大值;
是最大值;
当 ![]() ,即
,即 ![]() 点在右端点
点在右端点 ![]() 上时,
上时, ![]() 是最小值.
是最小值.