 设为首页
设为首页
 加入收藏
加入收藏
教学设计示例(一)
椭圆上点的特性
教学目标
(1)使学生进一步熟悉椭圆的定义、椭圆的方程、椭圆的性质及其应用;
(2)使学生做利用代数方法研究几何问题的初步尝试,掌握解析几何的基本思想方法.
教学重点 椭圆上点的特性.
教学过程
复习椭圆的定义及椭圆的方程.
问题1 在椭圆 ![]() 上求一点
上求一点 ![]() ,使
,使 ![]() ,其中
,其中 ![]() ,
, ![]() 是椭圆的两焦点.
是椭圆的两焦点.
请同学设计解题方案:
方案一:设 ![]() ,由题意得,
,由题意得,
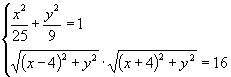 ,解方程组求出
,解方程组求出 ![]() .
.
(此方案是利用椭圆上的点的坐标满足椭圆的方程这一性质.)
方案二:由题意得,
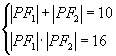 ,解方程得,
,解方程得, 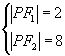 或
或 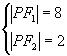 .
.
再设 ![]() ,则有
,则有 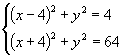 或
或 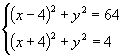 ,
,
解方程即可.
(此方案是利用椭圆上的点满足椭圆的第一定义这一性质.)
方案三:设 ![]() ,由椭圆
,由椭圆 ![]() 的第二定义得,
的第二定义得,
![]() ,
, ![]() ,
,
![]() ,
,
∴ ![]() ,
, ![]() ,
, ![]() .
.
(此方案是利用椭圆上的点满足椭圆的第二定义这一性质.)
问题2 设椭圆 ![]() 与两坐标轴的正向交于
与两坐标轴的正向交于 ![]() 、
、 ![]() ,在椭圆的
,在椭圆的 ![]() 弧上求一点
弧上求一点 ![]() ,使四边形
,使四边形 ![]() 的面积最大.
的面积最大.
请同学们设计解题方案.
方案一 设 ![]() 联结
联结 ![]() ,四边形
,四边形 ![]() 的面积可分为三角形
的面积可分为三角形 ![]() 和三角形
和三角形 ![]() .
.
![]()
![]()
![]()
![]() ,
,
![]() ,
,
∴ ![]()
∴ ![]() .
.
方案二 设 ![]() 联结
联结 ![]() ,四边形
,四边形 ![]() 的面积可分为三角形
的面积可分为三角形 ![]() 和三角形
和三角形 ![]() .
.
![]()
![]()
![]() .
.
教学设计示例(二)
椭圆的简单几何性质 (第一课时)
(一)教学目标
掌握椭圆的范围、对称性、顶点、离心率这四个几何性质,掌握标准方程中 ![]() 、
、 ![]() 以及
以及 ![]() 、
、 ![]() 的几何意义,
的几何意义, ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 之间的相互关系,明确怎样用代数的方法研究曲线的几何性质.
之间的相互关系,明确怎样用代数的方法研究曲线的几何性质.
(二)教学过程
【复习引入】
由学生口述,教师板书:
问题1.椭圆的标准方程是怎样的?
问题2.在直角坐标系内,关于 ![]() 轴、
轴、 ![]() 轴、原点对称的点的坐标之间有什么关系?
轴、原点对称的点的坐标之间有什么关系?
【探索研究】
1.椭圆的几何性质
根据曲线的方程研究曲线的几何性质,并正确地画出它的图形,是解析几何的基本问题之一.根据曲线的条件列出方程.如果说是解析几何的手段,那么根据曲线的方程研究曲线的性质、画图、就可以说是解析几何的目的.
下面我们根据椭圆的标准方程 ![]()
![]() 来研究椭圆的几何性质.
来研究椭圆的几何性质.
(1)范围
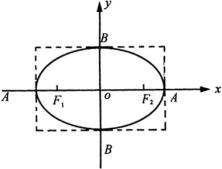 引导学生从标准方程
引导学生从标准方程
![]() ,得出不等式
,得出不等式 ![]() ,
, ![]() ,即
,即 ![]() ,
, ![]() .这说明椭圆的直线
.这说明椭圆的直线 ![]() 和直线
和直线 ![]() 所围成的矩形里(如图),注意结合图形讲解,并指出描点画图时,就不能取范围以外的点.
所围成的矩形里(如图),注意结合图形讲解,并指出描点画图时,就不能取范围以外的点.
(2)对称性
先让学生阅读教材中椭圆的几何性质2.
设问:为什么“把 ![]() 换成
换成 ![]() ,或把
,或把 ![]() 换
换 ![]() ,或把
,或把 ![]() 、
、 ![]() 同时换成
同时换成 ![]() 、
、 ![]() 时,方程解不变.则图形关于
时,方程解不变.则图形关于 ![]() 轴、
轴、 ![]() 轴或原点对称”呢?
轴或原点对称”呢?
事实上,在曲线方程里,如果把 ![]() 换成
换成 ![]() ,而方程不变,那么当点
,而方程不变,那么当点 ![]()
![]() 在曲线上时,点
在曲线上时,点 ![]() 关于
关于 ![]() 轴的对称点
轴的对称点 ![]() 也在曲线上,所以曲线关于
也在曲线上,所以曲线关于 ![]() 轴对称.类似地可以证明其他两个命题.
轴对称.类似地可以证明其他两个命题.
同时应向学生指出:如果曲线具有关于 ![]() 轴对称,关于
轴对称,关于 ![]() 轴对称和关于原点对称中的任意两种,那么它一定具有另一种对称.
轴对称和关于原点对称中的任意两种,那么它一定具有另一种对称.
最后强调: ![]() 轴、
轴、 ![]() 轴是椭圆的对称轴.原点是椭圆的对称中心即椭圆中心.进而说明椭圆的中心是焦点连线的中点,对称轴是焦点的连线及其中垂线与坐标系无关.因而是曲线的固有性质.
轴是椭圆的对称轴.原点是椭圆的对称中心即椭圆中心.进而说明椭圆的中心是焦点连线的中点,对称轴是焦点的连线及其中垂线与坐标系无关.因而是曲线的固有性质.
(3)顶点
引导学生从椭圆的标准方程 ![]() 分析它与
分析它与 ![]() 轴、
轴、 ![]() 轴的交点,只须令
轴的交点,只须令 ![]() 得
得 ![]() ,点
,点 ![]() 、
、 ![]() 是椭圆与
是椭圆与 ![]() 轴的两个交点;令
轴的两个交点;令 ![]() 得
得 ![]() ,点
,点 ![]() 、
、 ![]() 是椭圆与
是椭圆与 ![]() 轴的两个交点.应该强调:椭圆有四个顶点
轴的两个交点.应该强调:椭圆有四个顶点 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() .
.
同时还需指出:
(1°)线段 ![]() 和
和 ![]() 分别叫做椭圆的长轴和短轴,它们的长分别等于
分别叫做椭圆的长轴和短轴,它们的长分别等于 ![]() 和
和 ![]() ;
;
(2°) ![]() 、
、 ![]() 的几何意义:
的几何意义: ![]() 是椭圆长半轴的长,
是椭圆长半轴的长, ![]() 是椭圆短半轴的长.
是椭圆短半轴的长.
(3°)椭圆的顶点即是椭圆与对称轴的交点,一般二次曲线的顶点即是曲线与其对称轴的交点.
这时教师可作如下小结:由椭圆的范围,对称性和顶点,再进行描点画图,只须描出较少的点,就可以得到较正确的图形.
(4)离心率
由于离心率的概念比较抽象,教师可直接给出离心率的定义:
椭圆的焦距与长轴长的比 ![]() ,叫做椭圆的离心率.
,叫做椭圆的离心率.
先分析离心率 ![]() 的取值范围:
的取值范围:
∵ ![]() , ∴
, ∴ ![]() .
.
再结合图表分析离心率的大小对椭圆形状的影响:
(1)当 ![]() 趋近于1时,
趋近于1时, ![]() 趋近于
趋近于 ![]() ,从而
,从而 ![]() 越小,因此椭圆越扁平:
越小,因此椭圆越扁平:
(2)当 ![]() 趋近于0时,
趋近于0时, ![]() 趋近于0,从而
趋近于0,从而 ![]() 趋近于
趋近于 ![]() ,因此椭圆越接近于圆.
,因此椭圆越接近于圆.
【例题分析】
例1 求椭圆 ![]() 的长轴和短轴的长、离心率、焦点和顶点的坐标,并用描点法画出它的图形.
的长轴和短轴的长、离心率、焦点和顶点的坐标,并用描点法画出它的图形.
分析:只要化为椭圆的标准方程即可求解.
解:把已知方程化成标准方程是
![]()
这里 ![]() ,
, ![]() ,∴
,∴ ![]() .
.
因此,椭圆的长轴和短轴的长分别是 ![]() 和
和 ![]() ,离心率
,离心率 ![]() ,两个焦点分别是
,两个焦点分别是 ![]() 和
和 ![]() ,椭圆的四个顶点是
,椭圆的四个顶点是 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() .
.
(前一部分请一位学生板演,教师予以纠正,后一部分教师讲解,以引起学生重视.)步骤如下:
①列表:将已知方程变形为 ![]() ,
,
根据
![]() ,
,
在 ![]() 的范围内算出几个点的坐标
的范围内算出几个点的坐标 ![]() .
.
|
|
0 |
1 |
2 |
3 |
4 |
5 |
|
|
4 |
3.9 |
3.7 |
3.2 |
2.4 |
0 |
②描点作图:先描点画出椭圆在第一象限内的图形,再利用椭圆的对称性就可以画出整个椭圆(如图).
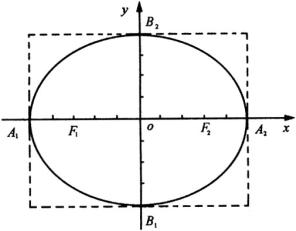
例2 求适合下列条件的椭圆的标准方程
(1)经过点 ![]() ,
, ![]() ;
;
(2)长轴长等于20,离心率等于 ![]() .
.
解:由椭圆的几何性质可知, ![]() 、
、 ![]() 分别是椭圆长轴和短轴的一个端点,于是得
分别是椭圆长轴和短轴的一个端点,于是得 ![]() ,
, ![]() .又因为长轴在
.又因为长轴在 ![]() 轴上,所以所求椭圆的标准方程为
轴上,所以所求椭圆的标准方程为 ![]() .
.
(2)由已知得 ![]() ,
, ![]() ∴
∴ ![]() ,
, ![]() ∴
∴ ![]() .
.
由于椭圆的焦点可能在 ![]() 轴上,也可能在
轴上,也可能在 ![]() 轴上,所以所求椭圆的标准方程为
轴上,所以所求椭圆的标准方程为 ![]() 或
或 ![]() .
.
(三)随堂练习
1.在下列方程所示的曲线中,关于 ![]() 轴、
轴、 ![]() 轴都对称的是( )
轴都对称的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
2.求下列各椭圆的长轴和短轴的长、离心率、焦点坐标、顶点坐标,并画出草图① ![]() ②
② ![]() .
.
3.下列每组椭圆中,哪一个更接近于圆
① ![]() 与
与 ![]() ;
;
② ![]() 与
与 ![]() .
.
答案:1.D 2.① ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .②
.② ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,图略.
,图略.
3.① ![]() ②
② ![]() .
.
(四)总结提炼
| 方程 |
|
|
| 图形 |
|
|
| 范围 |
|
|
| 对称性 |
关于 |
关于 |
| 顶点 |
|
|
| 离心率 |
|
|
(五)布置作业
1.椭圆 ![]() 的长轴的端点坐标是( )
的长轴的端点坐标是( )
A. ![]() ,
, ![]() B.
B. ![]() ,
, ![]()
C. ![]() ,
, ![]() D.
D. ![]() ,
, ![]()
2.椭圆 ![]() 与
与 ![]() 的关系为( )
的关系为( )
A.有相等的长、短轴 B.有相等的焦距
C.有相同的焦点 D.有相同的准线
3.中心在原点、焦点在 ![]() 轴上,若长轴长为18,且两个焦点恰好将长轴三等分,则此椭圆的方程是( )
轴上,若长轴长为18,且两个焦点恰好将长轴三等分,则此椭圆的方程是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
4.椭圆 ![]() 的长轴长为______________,短轴长为_______________,焦点坐标为_______________,离心率为_______________.
的长轴长为______________,短轴长为_______________,焦点坐标为_______________,离心率为_______________.
5.求适合下列条件的椭圆的标准方程
(1)椭圆经过两点 ![]() ,
, ![]() ;
;
(2)长轴是短轴的3倍,椭圆经过点
![]() ;
;
(3)离心率等于0.8,焦距是8.
答案:1.D 2.B 3.A 4.10、2, ![]() 、
、 ![]() ,
, ![]() 5.(1)
5.(1) ![]() (2)
(2) ![]() 或
或 ![]() (3)
(3) ![]() 或
或 ![]()
(六)板书设计
| 8.2 椭圆的简单几何性质(一) |
||
|
(一)复习提问 问题1 问题2 (二)椭圆的几何性质 1. 2. 3. 4. |
(三)例题与练习 例1 例2 |
练习 (四)小结 |
教学设计示例(三)
椭圆的简单几何性质 第二课时
(一)教学目标
进一步掌握椭圆的几何性质,掌握椭圆的第二定义,能应用椭圆的第二定义解决椭圆的有关问题,明确椭圆的第一定义与椭圆的第二定义是等价的,可以互相推出.
(二)教学过程
【复习引入】
前一节学习了椭圆的几何性质,哪一位同学回答:
问题1.椭圆有哪些几何性质?
问题2.什么叫做椭圆的离心率?
以上两个问题学生的回答应该不会有大的问题.教师可进一步提出问题:离心率的几何意义是什么呢?让我们先来看一个问题.
点 ![]() 与定点
与定点 ![]() 的距离和它到定直线
的距离和它到定直线 ![]() 的距离的比是常数
的距离的比是常数 ![]() (
( ![]() ),求点
),求点 ![]() 的轨迹.
的轨迹.
【探索研究】
椭圆的第二定义.
(按求轨迹方程的步骤,学生回答,教师板演.)
解:设 ![]() 是点
是点 ![]() 直线
直线 ![]() 的距离,根据题意,如图所求轨迹就是集合
的距离,根据题意,如图所求轨迹就是集合
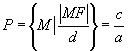
由此得 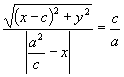 .
.
将上式两边平方,并化简得 ![]()
设 ![]() ,就可化成
,就可化成 ![]()
![]()
这是椭圆的标准方程,所以点 ![]() 的轨迹是长轴长为
的轨迹是长轴长为 ![]() ,短轴长为
,短轴长为 ![]() 的椭圆.
的椭圆.
由此可知,当点 ![]() 与一个定点的距离和它到一条定直线的距离的比是常数
与一个定点的距离和它到一条定直线的距离的比是常数 ![]() 时,这个点的轨迹是椭圆,一般称为椭圆的第二定义,定点是椭圆的焦点,定直线叫做椭圆的准线,常数
时,这个点的轨迹是椭圆,一般称为椭圆的第二定义,定点是椭圆的焦点,定直线叫做椭圆的准线,常数 ![]() 是椭圆的离心率.
是椭圆的离心率.
对于椭圆 ![]()
![]() ,相应于焦点
,相应于焦点 ![]() 的准线方程是
的准线方程是 ![]() .根据椭圆的对称性,相应于焦点
.根据椭圆的对称性,相应于焦点 ![]() 的准线方程是
的准线方程是 ![]() ,所以椭圆有两条准线.
,所以椭圆有两条准线.
可见椭圆的离心率就是椭圆上一点到焦点的距离与到相应准线距离的比,这就是离心率的几何意义.
至此教师可列出下表,由学生归纳.
|
图形 |
|
|
|
|
相同点 |
长轴长
|
||
|
不同点 |
方程 |
|
|
| 焦点 |
|
|
|
| 顶点 |
|
|
|
| 准线 |
|
|
|
【例题分析】
例1 求椭圆 ![]() 的长轴与短轴的长、焦点坐标、顶点坐标、离心率和准线方程.可请一位学生演板,教师纠正,答案为
的长轴与短轴的长、焦点坐标、顶点坐标、离心率和准线方程.可请一位学生演板,教师纠正,答案为
![]() ,
, ![]() ,焦点
,焦点 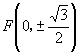 ,顶点
,顶点 ![]() ,
, ![]() ,
, ![]() ,准线方程
,准线方程 ![]() .
.
例2 已知椭圆 ![]() 上一点
上一点 ![]() 到其左、右焦点距离的比为1:3,求
到其左、右焦点距离的比为1:3,求 ![]() 点到两条准线的距离.
点到两条准线的距离.
可在学生练习后请一位学生回答.解答如下:
由椭圆标准方程可知
![]() ,
, ![]() ,∴
,∴
![]() ,
, ![]() .
.
由于 ![]() ,
, ![]() .
.
∴ ![]() ,
, ![]() .
.
设 ![]() 到左准线与右准线的距离分别为
到左准线与右准线的距离分别为 ![]() 与
与 ![]() ,根据椭圆的第二定义,有
,根据椭圆的第二定义,有 ![]()
∴ ![]() ,
, ![]() .
.
即 ![]() 到左准线的距离为
到左准线的距离为 ![]() ,到右准线的距离为
,到右准线的距离为 ![]() .
.
例3 已知椭圆 ![]() 内有一点
内有一点 ![]() ,
, ![]() 是椭圆的
是椭圆的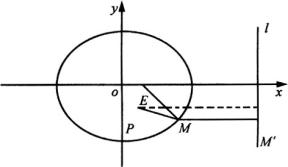 右焦点,在椭圆上有一点
右焦点,在椭圆上有一点 ![]() ,使
,使 ![]() 的值最小,求
的值最小,求 ![]() 的坐标.(如图)
的坐标.(如图)
分析:若设
![]() ,求出
,求出 ![]() ,再计算最小值是很繁的.由于
,再计算最小值是很繁的.由于 ![]() 是椭圆上一点到焦点的距离,由此联想到椭圆的第二定义,它与到相应准线的距离有关.故有如下解法.
是椭圆上一点到焦点的距离,由此联想到椭圆的第二定义,它与到相应准线的距离有关.故有如下解法.
解:设 ![]() 在右准线
在右准线 ![]() 上的射影为
上的射影为 ![]() .
.
由椭圆方程可知
![]() ,
, ![]()
![]() ,
, ![]() .
.
根据椭圆的第二定义,有 ![]()
即 ![]() .
.
∴ ![]() .
.
显然,当 ![]() 、
、 ![]() 、
、 ![]() 三点共线时,
三点共线时, ![]() 有最小值.
有最小值.
过 ![]() 作准线的垂线
作准线的垂线 ![]() .
.
由方程组 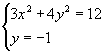 解得
解得 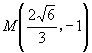 .
.
即 ![]() 的坐标为
的坐标为 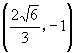 .
.
(三)随堂练习
1.若椭圆两准线间的距离等于焦距的4倍,则这个椭圆的离心率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
2.已知椭圆方程 ![]() 的一条准线方程是
的一条准线方程是 ![]() ,则
,则 ![]() 的值是( )
的值是( )
A.1 B.2 C.3 D.7
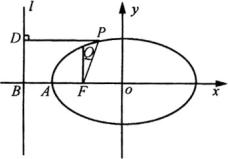 3.如图,
3.如图, ![]() 为椭圆的中心,
为椭圆的中心, ![]() 为焦点,
为焦点, ![]() 为顶点,准线
为顶点,准线 ![]() 交
交 ![]() 于
于 ![]() ,
, ![]() 、
、 ![]() 在椭圆上,
在椭圆上, ![]() 于
于 ![]() ,
, ![]() 于
于 ![]() .设椭圆的离心率为
.设椭圆的离心率为 ![]() ,则
,则
① ![]() ;
②
;
② ![]() ;
;
③ ![]() ;
④
;
④ ![]() ;
;
⑤ ![]() .
.
其中正确的个数是( ).
A.2个 B.3个 C.4个 D.5个
答案:1.D 2.A 3.D
(四)总结提炼
1.列出椭圆的几何意义.(投影展示上表).
2.通过椭圆的第二定义,可进一步了解椭圆的离心率的几何意义,它反映椭圆的圆扁程度,决定着椭圆的形状.两准线间的距离为 ![]() 是不变量.
是不变量.
(五)布置作业
1.椭圆 ![]() 的准线方程是( )
的准线方程是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
2.椭圆两焦点和中心将两准线间的距离四等分,则一焦点与短轴两端点连线的夹角是( )
A.45° B.60° C.90° D.120°
3.椭圆 ![]() 上的点
上的点 ![]() 到它的左准线的距离是10,那么
到它的左准线的距离是10,那么 ![]() 到它右焦点的距离是( )
到它右焦点的距离是( )
A.15 B.12 C.10 D.8
4.中心在原点,离心率为 ![]() ,且一条准线方程是
,且一条准线方程是 ![]() 的椭圆方程是_____________.
的椭圆方程是_____________.
5.求两对称轴都与坐标轴重合,离心率 ![]() ,焦点与相应准线的距离等于
,焦点与相应准线的距离等于 ![]() 的椭圆方程.
的椭圆方程.
6.点 ![]() 与定点
与定点 ![]() 的距离和它到定直线
的距离和它到定直线 ![]() 的距离的比是1:2,求点
的距离的比是1:2,求点 ![]() 的轨迹方程,并说明轨迹是什么图形.
的轨迹方程,并说明轨迹是什么图形.
答案:1.D 2.C 3.B
4. ![]() 5.
5. ![]() 或
或 ![]() 6.
6. ![]() ,轨迹为椭圆.
,轨迹为椭圆.
(六)板书设计
|
8.2 椭圆的简单几何性质(二) |
||
|
(一)复习提问 问题1 问题2 (二)椭圆的第二定义 |
(三)例题与练习 例1 例2 例3 |
学生练习 (四)小结 |
教学设计示例(四)
椭圆的简单几何性质(第三课时)
(一)教学目标
1.能利用椭圆中的基本量
![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 熟练地求椭圆的标准方程.
熟练地求椭圆的标准方程.
2.掌握椭圆的参数方程,会用参数方程解一些简单的问题.
(二)教学过程
【复习引入】
由一位学生回答,教师板书列表或用投影仪给出.
问题1.椭圆有哪些几何性质?
问题2.确定椭圆的标准方程需要几个条件?
通过对椭圆标准方程的讨论,研究了椭圆的几何性质,必须掌握标准方程中
![]() 、
、 ![]() 和
和 ![]() 、
、 ![]() 的几何意义以及
的几何意义以及 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 之间的相互关系,这样就可以由椭圆的几何性质确定它的标准方程.
之间的相互关系,这样就可以由椭圆的几何性质确定它的标准方程.
【例题分析】
例1 求中心在原点,过点
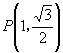 ,一条准线方程为
,一条准线方程为 ![]() 的椭圆方程.
的椭圆方程.
分析:根据准线方程可知椭圆的焦点在
![]() 轴上,由于思路不同有两种不同的解法,可让学生练习后,教师再归纳小结,解法如下:
轴上,由于思路不同有两种不同的解法,可让学生练习后,教师再归纳小结,解法如下:
解法一:设椭圆方程为 ![]() .
.
∵点 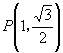 在椭圆上
在椭圆上
∴ ![]() 即
即 ![]() ①
①
又∵一条准线方程是 ![]()
∴ ![]()
![]() ②
②
将①、②代入
![]() ,得
,得
![]() 整理得
整理得 ![]()
解得 ![]() 或
或 ![]() .
.
分别代入①得 ![]() 或
或 ![]() .
.
故所求椭圆方程为 ![]() 或
或 ![]() .
.
解法二:设椭圆的右焦点为
![]() ,点
,点 ![]() 到椭圆右准线的距离为
到椭圆右准线的距离为 ![]() ,由椭圆的第二定义得
,由椭圆的第二定义得 ![]() ,即
,即
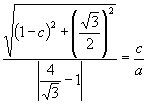 .
①
.
①
又由准线方程为 ![]()
![]() .
②
.
②
将②代入①,整理得
![]()
解得 ![]() 或
或 ![]() .
.
代入②及 ![]() 得
得
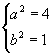 或
或
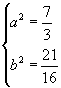
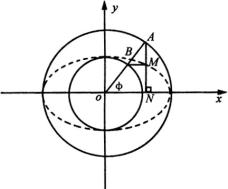 故所求椭圆的方程为
故所求椭圆的方程为 ![]() 或
或 ![]() .
.
例2 如图,以原点心圆心,分别以
![]() 、
、 ![]()
![]() 为半径作两个圆,点
为半径作两个圆,点 ![]() 是大圆半径
是大圆半径 ![]() 与小圆的交点,过点
与小圆的交点,过点 ![]() 作
作 ![]() ,垂足为
,垂足为 ![]() ,过点
,过点 ![]() 作
作 ![]() ,垂足为
,垂足为 ![]() ,求当半径
,求当半径 ![]() 绕点
绕点 ![]() 旋转时点
旋转时点 ![]() 的轨迹的参数方程.
的轨迹的参数方程.
解:设点 ![]() 的坐标为
的坐标为 ![]() ,
, ![]() 是以
是以 ![]() 为始边,
为始边, ![]() 为终边的正角.
为终边的正角.
取 ![]() 为参数,那么
为参数,那么 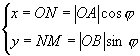
即 ![]()
这就是所求点 ![]() 的轨迹的参数方程.
的轨迹的参数方程.
消去参数 ![]() 后得到
后得到 ![]() ,由此可知,点
,由此可知,点 ![]() 的轨迹是椭圆.
的轨迹是椭圆.
点评:这道题还给出了椭圆的一种画法,按照这种方法,在已知椭圆的长、短轴长的情况下,给出离心角
![]() 的一个值,就可以画出椭圆上的一个对应点,利用几何画板画椭圆都用此法.
的一个值,就可以画出椭圆上的一个对应点,利用几何画板画椭圆都用此法.
例3 已知椭圆
![]() ,(
,( ![]() ,
, ![]() ,
, ![]() 为参数)上的点
为参数)上的点 ![]() ,求:
,求:
(1) ![]() 、
、 ![]() 的取值范围;
的取值范围;
(2) ![]() 的取值范围.
的取值范围.
解:(1)∵ ![]() ,
, ![]() ,
,
∴ ![]() ,
, ![]() .
.
∴ ![]() ,
, ![]() 为所求范围.
为所求范围.
(2)∴ ![]()
![]() .
.
(其中 ![]() 为第一象限角,且
为第一象限角,且 ![]() ).
).
而 ![]() .
.
∴ ![]() ,
,
即 ![]() 这所求.
这所求.
例4 把参数方程
![]() (
( ![]() 为参数).写成普通方程,并求出离心率.
为参数).写成普通方程,并求出离心率.
解:由参数方程得 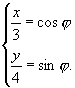
平方相加得 ![]() 为所求普通方程.
为所求普通方程.
∵ ![]() ,
, ![]() ,
,
∴ ![]() .
.
∴椭圆的离心率 ![]() .
.
(三)随堂练习
1.焦点在 ![]() 轴上的椭圆上一点
轴上的椭圆上一点 ![]() 到两准线间的距离之和为36,到两焦点的距离分别为9和15的椭圆的标准方程为______________.
到两准线间的距离之和为36,到两焦点的距离分别为9和15的椭圆的标准方程为______________.
2.参数方程 ![]() (
( ![]() 为参数)表示的曲线的焦点坐标是______________.
为参数)表示的曲线的焦点坐标是______________.
3.椭圆 ![]() (
( ![]() 为参数)的离心率为_________________.
为参数)的离心率为_________________.
答案:1. ![]() 2.
2. ![]() ,
, ![]() 3.
3. ![]()
(四)总结提炼
1.求曲线方程的基本程序是
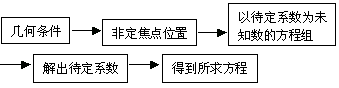
若已知条件涉及到焦点,准线方程式时,往往利用定义求解较简便.
2.椭圆的参数方程 ![]() (
( ![]() 为参数)中,
为参数)中, ![]() 表明
表明 ![]() 、
、 ![]() 分别是椭圆的长轴、短轴长,且焦点在
分别是椭圆的长轴、短轴长,且焦点在 ![]() 轴上,参数
轴上,参数 ![]() 的几何意义是椭圆的离心角,利用椭圆的参数方程求
的几何意义是椭圆的离心角,利用椭圆的参数方程求
![]() 的最值较方便.
的最值较方便.
(五)布置作业
1.已知椭圆中心在原点,一个焦点是
![]() ,点
,点 ![]() 在椭圆上,则点
在椭圆上,则点 ![]() 到与
到与 ![]() 相应准线的距离为(
)
相应准线的距离为(
)
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
2.椭圆 ![]()
![]() 的左焦点为
的左焦点为 ![]() ,
, ![]() ,
, ![]() 是两个顶点,如果
是两个顶点,如果 ![]() 到直线
到直线 ![]() 的距离等于
的距离等于 ![]() ,那么椭圆的离心率等于(
)
,那么椭圆的离心率等于(
)
A. ![]() B.
B.
![]() C.
C. ![]() D.
D. ![]()
4.椭圆 ![]() (
( ![]() 为参数)的两准线间距离为_______________.
为参数)的两准线间距离为_______________.
5.已知椭圆的一条准线方程是
![]() ,且过点
,且过点 ![]() ,求椭圆的标准方程.
,求椭圆的标准方程.
6.求椭圆 ![]()
![]() 的内接矩形面积的最大值.
的内接矩形面积的最大值.
答案:1.A 2.C
3.D 4. ![]() 5.
5. ![]()
7.设 ![]() 是椭圆上的任一点,则
是椭圆上的任一点,则 ![]() (
( ![]() 为参数)
为参数)
内接矩形面积 ![]()
![]()
∴ ![]()
![]() .
.
(六)板书设计
|
8.2 椭圆的简单几何性质(三) |
||
|
一、复习引入 二、例题分析 例1 |
例2 例3 例4 |
练习 总结 |
教学设计示例(五)
椭圆的简单几何性质 (第四课时)
(一)教学目标
1.能推导并掌握椭圆的焦半径公式,能利用焦半径公式解决有关与焦点距离有关的问题.
2.能利用椭圆的有关知识解决实际应用问题.
3.能综合利用椭圆的有关知识,解决最值问题及参数的取值范围问题.
(二)教学过程
【复习引入】
1.利用投影仪显示椭圆的定义,标准方程及其几何性质(见第二课时).
2.求椭圆上到焦点距离的最大值与最小值.
【探索研究】
为研究上述问题,可先解决例1,教师出示问题.
例1 求证:椭圆 ![]()
![]() 上任一点
上任一点 ![]() 与焦点所连两条线段的长分别为
与焦点所连两条线段的长分别为 ![]() .
.
分析:由距离公式和椭圆定义可以有两种证法,先由一位学生演板,教师最后予以补充.
证法一:设椭圆的左、右焦点分别为 ![]() .
. ![]() ,则
,则
![]()
![]()
![]()
∵ ![]() , ∴
, ∴ ![]() .
.
∴ ![]() .
.
又 ![]() ,
,
∴ ![]() 故得证.
故得证.
证法二:设 ![]() 到左右准线的距离分别为
到左右准线的距离分别为 ![]() ,
, ![]() ,由椭圆的第二定义有
,由椭圆的第二定义有
![]() ,
,
又 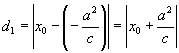 ,
,
∴ 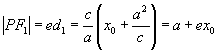 .
.
又 ![]() ,
,
∴ ![]() . 故得证.
. 故得证.
说明: ![]() 、
、 ![]() 叫做椭圆的焦半径.利用焦半径公式在椭圆的有关计算、证明中,能大大简化相应的计算.至此可解决开始提出的问题.
叫做椭圆的焦半径.利用焦半径公式在椭圆的有关计算、证明中,能大大简化相应的计算.至此可解决开始提出的问题.
∵ ![]() ,
, ![]() ,
,
∴ ![]() ,
, ![]() .
.
∴ ![]() .
.
即椭圆上焦点的距离最大值为 ![]() ,最小值为
,最小值为 ![]() ,最大值与最小值点即是椭圆长轴上的顶点.
,最大值与最小值点即是椭圆长轴上的顶点.
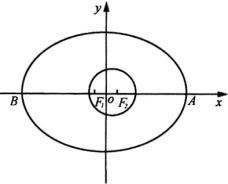 例2 如图,我国发射的第一颗人造地球卫星的运行轨道是以地心(地球中心)
例2 如图,我国发射的第一颗人造地球卫星的运行轨道是以地心(地球中心) ![]() 为一个焦点的椭圆.已知它们近地点
为一个焦点的椭圆.已知它们近地点 ![]() (离地面最近的点)距地面439
(离地面最近的点)距地面439 ![]() ,远地点
,远地点 ![]() (离地面最)距地面2384
(离地面最)距地面2384 ![]() ,并且
,并且 ![]() 、
、 ![]() 、
、 ![]() 在同一条直线上,地球半径约6371
在同一条直线上,地球半径约6371 ![]() ,求卫星运行的轨道方程(精确到1
,求卫星运行的轨道方程(精确到1 ![]() ).
).
分析:这是一个介绍椭圆在航天领域应用的例子,关键是理解近地点和远地点与椭圆的关系.由于数字大,计算较繁,可教师讲解.
解:如图,建立直角坐标系,使点 ![]() 、
、 ![]() 、
、 ![]() 在
在 ![]() 轴上,
轴上, ![]() 为椭圆的右焦点(记
为椭圆的右焦点(记 ![]() 为左焦点).
为左焦点).
因为椭圆的焦点在 ![]() 轴上,所以设它的方程为
轴上,所以设它的方程为 ![]()
![]()
则 ![]()
![]()
解得 ![]()
![]()
∴ ![]() .
.
因此,卫星的轨道方程是 ![]() .
.
点评:由例1可知椭圆上到焦点的距离的最大和最小的点,恰是椭圆长轴的两个端点,因而可知所有卫星的近地点、远地点、及轨道的焦点都在同一直线上.
例3 已知点 ![]() 在圆
在圆 ![]() 上移动,点
上移动,点 ![]() 在椭圆
在椭圆 ![]() 上移动,求
上移动,求 ![]() 的最大值.
的最大值.
分析:要求 ![]() 的最大值,只要考虑圆心到椭圆上的点的距离,而椭圆上的点是有范围的.可在教师指导下学生完成,解答如下:
的最大值,只要考虑圆心到椭圆上的点的距离,而椭圆上的点是有范围的.可在教师指导下学生完成,解答如下:
设椭圆上一点 ![]() ,又
,又 ![]() ,于是
,于是
![]()
![]()
![]() .
.
而 ![]()
∴当 ![]() 时,
时, ![]() 有最大值5.
有最大值5.
故 ![]() 的最大值为6.
的最大值为6.
点评:椭圆中的最值问题常转化为二次函数在闭区间上的最值问题.
例4 已知椭圆 ![]()
![]() 与
与 ![]() 轴的正半轴交于点
轴的正半轴交于点 ![]() ,
, ![]() 是原点.若椭圆上存在一点
是原点.若椭圆上存在一点 ![]() ,使
,使 ![]() ,求椭圆离心率
,求椭圆离心率 ![]() 的取值范围.
的取值范围.
分析:依题意 ![]() 点的横坐标
点的横坐标 ![]() ,找到
,找到 ![]() 与
与 ![]() 、
、 ![]() 的关系式.教师讲解为好.
的关系式.教师讲解为好.
解:设 ![]() 的坐标为
的坐标为 ![]() ,由
,由 ![]() ,有
,有
![]()
于是下面方程组的解为 ![]() 的坐标
的坐标
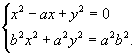
消去 ![]() 整理得
整理得
![]() .
.
解得 ![]() 或
或
![]() .
.
![]() 即为椭圆的右顶点
即为椭圆的右顶点
∴ ![]() 即
即 ![]() .
.
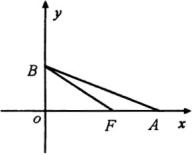 即
即 ![]() ,而
,而 ![]() ,
故
,
故 ![]() .
.
(三)随堂练习
1.如图在 ![]() 中,
中, ![]() ,
, ![]() ,则以
,则以 ![]() 为焦点,
为焦点, ![]() 、
、 ![]() 分别是长、短轴端点的椭圆方程是______________.
分别是长、短轴端点的椭圆方程是______________.
2.设椭圆 ![]() 上动点
上动点 ![]() 到定点
到定点 ![]()
![]() 的距离
的距离 ![]() 最小值为1,求
最小值为1,求 ![]() 的值.
的值.
答案:1. ![]() 2.
2. ![]()
(四)总结提炼
椭圆的焦半径是椭圆的基础问题,在解题中有其独特的作用,椭圆的范围在解决椭圆的元素的范围及与其有关的最大值(最小值)问题时是很有效的方法.
(五)布置作业
1.椭圆短半轴的长为1,离心率的最大值是 ![]() ,则长半轴长的取值范围是___________.
,则长半轴长的取值范围是___________.
2.若椭圆两焦点为 ![]() ,
, ![]() ,
, ![]() 在椭圆上,且
在椭圆上,且 ![]() 的最大面积是12,则椭圆方程是_______________.
的最大面积是12,则椭圆方程是_______________.
3.已知 ![]() 是椭圆
是椭圆 ![]()
![]() 的一个焦点,
的一个焦点, ![]() 是过其中心的一条弦,记
是过其中心的一条弦,记 ![]() ,则
,则 ![]() 面积的最大值是( )
面积的最大值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
4.已知 ![]() 是椭圆
是椭圆 ![]() 上的任意一点,以过
上的任意一点,以过 ![]() 的一条焦半径为直径作圆
的一条焦半径为直径作圆 ![]() ,以椭圆长轴为直径作圆
,以椭圆长轴为直径作圆 ![]() ,则圆
,则圆 ![]() 与圆
与圆 ![]() 的位置关系是( )
的位置关系是( )
A.内切 B.内含 C.相交 D.相离
5.设 ![]() 是椭圆
是椭圆 ![]()
![]() 上的任一点,求
上的任一点,求 ![]() 点到椭圆两焦点
点到椭圆两焦点 ![]() 、
、 ![]() 距离之积的最大值与最大值,并求取得最大值与最小值时
距离之积的最大值与最大值,并求取得最大值与最小值时 ![]() 点的坐标.
点的坐标.
6.设椭圆的中心是坐标原点,长轴在 ![]() 轴上,离心率
轴上,离心率 ![]() ,已知点
,已知点 ![]() 到这个椭圆上的点的最远距离是
到这个椭圆上的点的最远距离是 ![]() ,求这个椭圆方程,并求椭圆上到点
,求这个椭圆方程,并求椭圆上到点 ![]() 的距离等于
的距离等于 ![]() 的点的坐标.
的点的坐标.
答案:1. ![]() 2.
2. ![]() 3.D
4.A
3.D
4.A
5.设 ![]() 则
则 ![]() ,
, ![]()
![]()
∵ ![]() ∴
∴ ![]()
当 ![]() 即
即 ![]() 或
或 ![]() 时,
时, ![]() 最大,最大值为
最大,最大值为 ![]() .
.
当 ![]() 即
即 ![]() 或
或 ![]() 时,
时, ![]() 最小,最小值为
最小,最小值为 ![]() .
.
6.设所求椭圆方程是 ![]()
![]()
依题意可得 ![]() ,其中
,其中 ![]()
如果 ![]() ,则当
,则当 ![]() 时,
时, ![]() 有最大值,即
有最大值,即 ![]() .
.
由此得 ![]() ,与
,与 ![]() 矛盾.
矛盾.
因此必有 ![]() 成立,于是当
成立,于是当 ![]() 时,
时, ![]() 有最大值,即
有最大值,即 ![]() .
.
由此得 ![]() ,
, ![]() ,故所求椭圆方程为
,故所求椭圆方程为 ![]() .
.
由 ![]() 代入椭圆方程得点
代入椭圆方程得点 ![]() 和
和 ![]() 到点
到点 ![]() 的距离都是
的距离都是 ![]() .
.
注:本题也可设椭圆的参数方程是 ![]() ,其中
,其中 ![]() ,
, ![]() ,利用三角函数求解.
,利用三角函数求解.
(六)板书设计
|
8.2 椭圆的简单几何性质(四) |
||
|
1.知识要点 2.椭圆的焦半径公式 3.例题分析 例1 |
例2 例3 |
例4 练习小结 |
教学设计示例(六)
椭圆的简单几何性质(第五课时)
(一)教学目标
理解直线与椭圆的位置关系,能判定直线与椭圆的位置关系,会求直线截椭圆所得的弦长,处理与弦长、弦的中点有关的问题.
(二)教学过程
【情境设置】
问题一:直线与圆的位置关系有几种?(相交、相切、相离),那么直线与椭圆的位置关系有几种?(仍是相交、相切、相离)
问题二:如何判断直线与圆的位置关系?又怎样判定直线与椭圆的位置关系呢?
(直线与圆位置关系有两种判定方法:一是根据圆心到直线的距离与圆的半径比较当 ![]() 时相交,当
时相交,当 ![]() 时相切,当
时相切,当 ![]() 时相离,另一种判别方法是直线与圆联立方程组,转化为一元二次方程根的判别式来解决,当
时相离,另一种判别方法是直线与圆联立方程组,转化为一元二次方程根的判别式来解决,当 ![]() 时,直线与圆相离直线与椭圆的位置关系应用一元二次方程根的判别式来解决.)
时,直线与圆相离直线与椭圆的位置关系应用一元二次方程根的判别式来解决.)
【探索研究】
1.练习:已知直线和椭圆的方程如下,求它们的交点坐标并说明位置关系.
(1) ![]() ,
, ![]()
(2) ![]() ,
, ![]()
答案:(1) ![]() 相切 (2)
相切 (2) ![]() ,
, ![]() ,相交.
,相交.
2.例题分析
例1 中心在原点,一个焦点为
![]() 的椭圆截直线
的椭圆截直线 ![]() 所得弦的中点横坐标为
所得弦的中点横坐标为 ![]() ,求椭圆的方程.
,求椭圆的方程.
由于学生接触类似的问题不多,可教师讲解.
解:设所求的椭圆方程为 ![]() ,
, ![]()
由 ![]() 得
得 ![]() ①
①
把直线方程 ![]() 代入椭圆方程,整理得
代入椭圆方程,整理得
![]()
设弦的两个端点为 ![]() ,
, ![]() ,则由根与系数关系得
,则由根与系数关系得
![]() .
.
又 ![]() 中点的横坐标为
中点的横坐标为 ![]() .
.
∴ ![]() .得
.得 ![]() ②
②
解①,②得 ![]() ,
, ![]() .
.
故所求椭圆的方程为 ![]() .
.
例2 过椭圆 ![]() 内一点
内一点 ![]() 引一条弦,使弦被
引一条弦,使弦被 ![]() 点平分,求这条弦所在直线的方程.
点平分,求这条弦所在直线的方程.
分析:本例与例1有相似之征,可让一位学生板演,再提问学生是否有不同的解法,然后教师归纳出以下三种解法:
解法一:设所求直线的方程为 ![]() ,代入椭圆方程并整理,得
,代入椭圆方程并整理,得
![]() .
.
设直线与椭圆的交点为 ![]() 、
、 ![]() ,则
,则 ![]() ,
, ![]() 是上述方程的两根,于是
是上述方程的两根,于是 ![]() .
.
又 ![]() 为
为 ![]() 的中点
的中点
∴ ![]() . 解得
. 解得 ![]() .
.
故所求直线的方程为 ![]() .
.
解法二:设直线与椭圆的交点为 ![]() 、
、 ![]() .
.
∵ ![]() 为
为 ![]() 的中点
的中点
∴ ![]() ,
, ![]() .
.
又 ![]() 、
、 ![]() 两点在椭圆上,则
两点在椭圆上,则
![]() ,
, ![]()
两式相减得
![]()
于是
![]() .
.
∴ 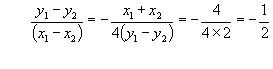
即 ![]()
故所求直线的方程为 ![]() .
.
解法三
设所求直线与椭圆的一个交点为
![]() ,由于中点为
,由于中点为 ![]() ,则另一个交点为
,则另一个交点为 ![]() .
.
∵ ![]() 、
、 ![]() 两点都在椭圆上.
两点都在椭圆上.
∴ ![]() .
①
.
①
![]() ②
②
①-②得
![]() .
.
由于过 ![]() 、
、 ![]() 的直线只有一条,故所求直线的方程为
的直线只有一条,故所求直线的方程为 ![]() .
.
例3 椭圆 ![]() ,与直线
,与直线 ![]() 相交于
相交于 ![]() 、
、 ![]() 两点,
两点, ![]() 是
是 ![]() 的中点.若
的中点.若 ![]() ,斜率为
,斜率为 ![]() (
( ![]() 为原点),试确定椭圆的方程.(如图)
为原点),试确定椭圆的方程.(如图)
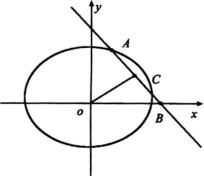 分析:注意利用弦长公式
分析:注意利用弦长公式
![]() ,因为计算比较复杂,可由教师讲解.
,因为计算比较复杂,可由教师讲解.
解法一:由方程组
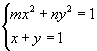 得
得 ![]()
设 ![]() 、
、 ![]() 、
、 ![]() ,则
,则
![]()
![]()
![]() .
.
∴ ![]() ,
, ![]()
由题设得 ![]() ①
①
又 ![]()
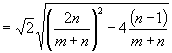
![]() ②
②
解①、②得 ![]() ,
, ![]() .∴椭圆方程为
.∴椭圆方程为 ![]() .
.
解法二:由 ![]() 得
得 ![]() 的方程为
的方程为 ![]() ,
,
由 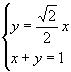 解得
解得 ![]() .
.
又由 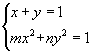 得
得 ![]() .
.
所以 ![]() 即
即 ![]() ①.
①.
又因为 ![]() 得
得 ![]() ②,
②,
由①、②求出 ![]() ,
, ![]()
故所求椭圆方程为 ![]() .
.
解法三:由 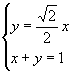 得
得 ![]() .
.
因为 ![]() ,所以直线的
,所以直线的 ![]() 的倾斜角为135°.
的倾斜角为135°.
又知 ![]() 是
是 ![]() 的中点,
的中点, ![]() ,所以
,所以 ![]() .
.
即 ![]() 同理求出点
同理求出点 ![]() .
.
将 ![]() 、
、 ![]() 坐标代入椭圆方程
坐标代入椭圆方程 ![]() ,
,
得 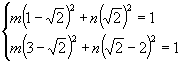 解得
解得 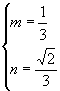 .
.
所以所求椭圆方程为 ![]() .
.
点拨:椭圆的两种形式的标准方程可统一写成 ![]() ,强以避免对焦点位置的讨论,且使运算过程简化,而弦中点问题常使用韦达定理来解决.
,强以避免对焦点位置的讨论,且使运算过程简化,而弦中点问题常使用韦达定理来解决.
(三)随堂练习
1.如果椭圆 ![]() 的弦被点
的弦被点 ![]() 平分,那么这条弦所在的直线的方程是( )
平分,那么这条弦所在的直线的方程是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
2.已知直线 ![]() ,椭圆
,椭圆 ![]()
(1)当 ![]() 为何值时,
为何值时, ![]() 与
与 ![]() 有两个不同的交点?没有交点?
有两个不同的交点?没有交点?
(2)当 ![]() 为何值时,直线
为何值时,直线 ![]() 被椭圆
被椭圆 ![]() 所截的弦长为
所截的弦长为 ![]() ?
?
答案:1.D 2.(1) ![]() ,
, ![]() 或
或 ![]() (2)
(2) ![]()
(四)总结提炼
1.直线与椭圆的位置关系,一般是通过方程组转化为一元二次方程,运用一元二次方程的知识(如求根、判别式、根与系数关系)求得.
2.要注意二次曲线与二次方程,二次函数三个二次之间的关系.
(五)布置作业
1.过点 ![]() 的直线
的直线 ![]() 与椭圆
与椭圆 ![]() 交于
交于 ![]() 、
、 ![]() 两点,线段
两点,线段 ![]()
![]() 的中点为
的中点为 ![]() ,设直线
,设直线 ![]() 的斜率为
的斜率为 ![]() ,直线
,直线 ![]() 的斜率为
的斜率为 ![]() ,则
,则 ![]() 的值等于( )
的值等于( )
A.2
B.-2 C. ![]() D.
D. ![]()
2.直线 ![]() 与椭圆
与椭圆 ![]() 恒有公共点,则
恒有公共点,则 ![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
3.已知椭圆 ![]() 的方程为
的方程为 ![]() ,如果直线
,如果直线 ![]() 与椭圆的一个交点
与椭圆的一个交点 ![]() 在
在 ![]() 轴上的射影恰好是椭圆的右焦点
轴上的射影恰好是椭圆的右焦点 ![]() ,则
,则 ![]() 的值为( )
的值为( )
A.2
B. ![]() C.
C. ![]() D.8
D.8
4.求与椭圆 ![]() 相交于
相交于 ![]() 、
、 ![]() 两点,并且线段
两点,并且线段 ![]() 的中点为
的中点为 ![]() 的直线方程.
的直线方程.
5.已知椭圆 ![]() 的焦点分别是
的焦点分别是 ![]() 、
、 ![]() ,过中心
,过中心 ![]() 作直线与椭圆相交于
作直线与椭圆相交于 ![]() 、
、 ![]() 两点,若要使
两点,若要使 ![]() 的面积是20,求该直线方程.
的面积是20,求该直线方程.
答案:1.D 2.C 3.B
4.设 ![]() 、
、 ![]() 的坐标分别为
的坐标分别为 ![]() ,
, ![]()
∵点 ![]() 、
、 ![]() 都在椭圆上
都在椭圆上
∴ 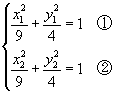
①-②得 ![]()
∵ ![]() 的中点为
的中点为 ![]() ∴
∴ ![]() ,
, ![]()
∴ ![]() ,即直线
,即直线 ![]() 的斜率为
的斜率为 ![]() .
.
∴所求直线方程为 ![]() 即
即 ![]()
5.易求得 ![]() ,设直线
,设直线 ![]() 方程为
方程为 ![]() ,代入椭圆方程得:
,代入椭圆方程得:
![]() 即
即 ![]()
∴ ![]() .
.
∴ ![]() .
.
由 ![]() 得
得 ![]() ,
,
∴直线 ![]() 的方程为
的方程为 ![]() 即
即 ![]() .
.
(六)板书设计
| 8.2 椭圆的简单几何性质(五) |
||
|
一、直线与椭圆的位置关系 二、例题分析 例1 |
例2 例3 |
练习 小结 |
教学设计示例(六)
椭圆的简单几何性质( 第五课时)
(一)教学目标
理解直线与椭圆的位置关系,能判定直线与椭圆的位置关系,会求直线截椭圆所得的弦长,处理与弦长、弦的中点有关的问题.
(二)教学过程
【情境设置】
问题一:直线与圆的位置关系有几种?(相交、相切、相离),那么直线与椭圆的位置关系有几种?(仍是相交、相切、相离)
问题二:如何判断直线与圆的位置关系?又怎样判定直线与椭圆的位置关系呢?
(直线与圆位置关系有两种判定方法:一是根据圆心到直线的距离与圆的半径比较当 ![]() 时相交,当
时相交,当 ![]() 时相切,当
时相切,当 ![]() 时相离,另一种判别方法是直线与圆联立方程组,转化为一元二次方程根的判别式来解决,当
时相离,另一种判别方法是直线与圆联立方程组,转化为一元二次方程根的判别式来解决,当 ![]() 时,直线与圆相离直线与椭圆的位置关系应用一元二次方程根的判别式来解决.)
时,直线与圆相离直线与椭圆的位置关系应用一元二次方程根的判别式来解决.)
【探索研究】
1.练习:已知直线和椭圆的方程如下,求它们的交点坐标并说明位置关系.
(1) ![]() ,
, ![]()
(2) ![]() ,
, ![]()
答案:(1) ![]() 相切 (2)
相切 (2) ![]() ,
, ![]() ,相交.
,相交.
2.例题分析
例1 中心在原点,一个焦点为
![]() 的椭圆截直线
的椭圆截直线 ![]() 所得弦的中点横坐标为
所得弦的中点横坐标为 ![]() ,求椭圆的方程.
,求椭圆的方程.
由于学生接触类似的问题不多,可教师讲解.
解:设所求的椭圆方程为 ![]() ,
, ![]()
由 ![]() 得
得 ![]() ①
①
把直线方程 ![]() 代入椭圆方程,整理得
代入椭圆方程,整理得
![]()
设弦的两个端点为 ![]() ,
, ![]() ,则由根与系数关系得
,则由根与系数关系得
![]() .
.
又 ![]() 中点的横坐标为
中点的横坐标为 ![]() .
.
∴ ![]() .得
.得 ![]() ②
②
解①,②得 ![]() ,
, ![]() .
.
故所求椭圆的方程为 ![]() .
.
例2 过椭圆 ![]() 内一点
内一点 ![]() 引一条弦,使弦被
引一条弦,使弦被 ![]() 点平分,求这条弦所在直线的方程.
点平分,求这条弦所在直线的方程.
分析:本例与例1有相似之征,可让一位学生板演,再提问学生是否有不同的解法,然后教师归纳出以下三种解法:
解法一:设所求直线的方程为 ![]() ,代入椭圆方程并整理,得
,代入椭圆方程并整理,得
![]() .
.
设直线与椭圆的交点为 ![]() 、
、 ![]() ,则
,则 ![]() ,
, ![]() 是上述方程的两根,于是
是上述方程的两根,于是 ![]() .
.
又 ![]() 为
为 ![]() 的中点
的中点
∴ ![]() . 解得
. 解得 ![]() .
.
故所求直线的方程为 ![]() .
.
解法二:设直线与椭圆的交点为 ![]() 、
、 ![]() .
.
∵ ![]() 为
为 ![]() 的中点
的中点
∴ ![]() ,
, ![]() .
.
又 ![]() 、
、 ![]() 两点在椭圆上,则
两点在椭圆上,则
![]() ,
, ![]()
两式相减得
![]()
于是
![]() .
.
∴ 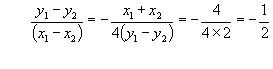
即 ![]()
故所求直线的方程为 ![]() .
.
解法三
设所求直线与椭圆的一个交点为
![]() ,由于中点为
,由于中点为 ![]() ,则另一个交点为
,则另一个交点为 ![]() .
.
∵ ![]() 、
、 ![]() 两点都在椭圆上.
两点都在椭圆上.
∴ ![]() .
①
.
①
![]() ②
②
①-②得
![]() .
.
由于过 ![]() 、
、 ![]() 的直线只有一条,故所求直线的方程为
的直线只有一条,故所求直线的方程为 ![]() .
.
例3 椭圆 ![]() ,与直线
,与直线 ![]() 相交于
相交于 ![]() 、
、 ![]() 两点,
两点, ![]() 是
是 ![]() 的中点.若
的中点.若 ![]() ,斜率为
,斜率为 ![]() (
( ![]() 为原点),试确定椭圆的方程.(如图)
为原点),试确定椭圆的方程.(如图)
 分析:注意利用弦长公式
分析:注意利用弦长公式
![]() ,因为计算比较复杂,可由教师讲解.
,因为计算比较复杂,可由教师讲解.
解法一:由方程组
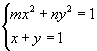 得
得 ![]()
设 ![]() 、
、 ![]() 、
、 ![]() ,则
,则
![]()
![]()
![]() .
.
∴ ![]() ,
, ![]()
由题设得 ![]() ①
①
又 ![]()
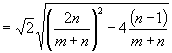
![]() ②
②
解①、②得 ![]() ,
, ![]() .∴椭圆方程为
.∴椭圆方程为 ![]() .
.
解法二:由 ![]() 得
得 ![]() 的方程为
的方程为 ![]() ,
,
由 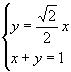 解得
解得 ![]() .
.
又由 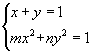 得
得 ![]() .
.
所以 ![]() 即
即 ![]() ①.
①.
又因为 ![]() 得
得 ![]() ②,
②,
由①、②求出 ![]() ,
, ![]()
故所求椭圆方程为 ![]() .
.
解法三:由 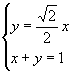 得
得 ![]() .
.
因为 ![]() ,所以直线的
,所以直线的 ![]() 的倾斜角为135°.
的倾斜角为135°.
又知 ![]() 是
是 ![]() 的中点,
的中点, ![]() ,所以
,所以 ![]() .
.
即 ![]() 同理求出点
同理求出点 ![]() .
.
将 ![]() 、
、 ![]() 坐标代入椭圆方程
坐标代入椭圆方程 ![]() ,
,
得 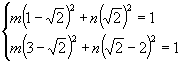 解得
解得 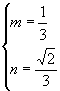 .
.
所以所求椭圆方程为 ![]() .
.
点拨:椭圆的两种形式的标准方程可统一写成 ![]() ,强以避免对焦点位置的讨论,且使运算过程简化,而弦中点问题常使用韦达定理来解决.
,强以避免对焦点位置的讨论,且使运算过程简化,而弦中点问题常使用韦达定理来解决.
(三)随堂练习
1.如果椭圆 ![]() 的弦被点
的弦被点 ![]() 平分,那么这条弦所在的直线的方程是( )
平分,那么这条弦所在的直线的方程是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
2.已知直线 ![]() ,椭圆
,椭圆 ![]()
(1)当 ![]() 为何值时,
为何值时, ![]() 与
与 ![]() 有两个不同的交点?没有交点?
有两个不同的交点?没有交点?
(2)当 ![]() 为何值时,直线
为何值时,直线 ![]() 被椭圆
被椭圆 ![]() 所截的弦长为
所截的弦长为 ![]() ?
?
答案:1.D 2.(1) ![]() ,
, ![]() 或
或 ![]() (2)
(2) ![]()
(四)总结提炼
1.直线与椭圆的位置关系,一般是通过方程组转化为一元二次方程,运用一元二次方程的知识(如求根、判别式、根与系数关系)求得.
2.要注意二次曲线与二次方程,二次函数三个二次之间的关系.
(五)布置作业
1.过点 ![]() 的直线
的直线 ![]() 与椭圆
与椭圆 ![]() 交于
交于 ![]() 、
、 ![]() 两点,线段
两点,线段 ![]()
![]() 的中点为
的中点为 ![]() ,设直线
,设直线 ![]() 的斜率为
的斜率为 ![]() ,直线
,直线 ![]() 的斜率为
的斜率为 ![]() ,则
,则 ![]() 的值等于( )
的值等于( )
A.2
B.-2 C. ![]() D.
D. ![]()
2.直线 ![]() 与椭圆
与椭圆 ![]() 恒有公共点,则
恒有公共点,则 ![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
3.已知椭圆 ![]() 的方程为
的方程为 ![]() ,如果直线
,如果直线 ![]() 与椭圆的一个交点
与椭圆的一个交点 ![]() 在
在 ![]() 轴上的射影恰好是椭圆的右焦点
轴上的射影恰好是椭圆的右焦点 ![]() ,则
,则 ![]() 的值为( )
的值为( )
A.2
B. ![]() C.
C. ![]() D.8
D.8
4.求与椭圆 ![]() 相交于
相交于 ![]() 、
、 ![]() 两点,并且线段
两点,并且线段 ![]() 的中点为
的中点为 ![]() 的直线方程.
的直线方程.
5.已知椭圆 ![]() 的焦点分别是
的焦点分别是 ![]() 、
、 ![]() ,过中心
,过中心 ![]() 作直线与椭圆相交于
作直线与椭圆相交于 ![]() 、
、 ![]() 两点,若要使
两点,若要使 ![]() 的面积是20,求该直线方程.
的面积是20,求该直线方程.
答案:1.D 2.C 3.B
4.设 ![]() 、
、 ![]() 的坐标分别为
的坐标分别为 ![]() ,
, ![]()
∵点 ![]() 、
、 ![]() 都在椭圆上
都在椭圆上
∴ 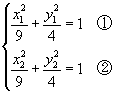
①-②得 ![]()
∵ ![]() 的中点为
的中点为 ![]() ∴
∴ ![]() ,
, ![]()
∴ ![]() ,即直线
,即直线 ![]() 的斜率为
的斜率为 ![]() .
.
∴所求直线方程为 ![]() 即
即 ![]()
5.易求得 ![]() ,设直线
,设直线 ![]() 方程为
方程为 ![]() ,代入椭圆方程得:
,代入椭圆方程得:
![]() 即
即 ![]()
∴ ![]() .
.
∴ ![]() .
.
由 ![]() 得
得 ![]() ,
,
∴直线 ![]() 的方程为
的方程为 ![]() 即
即 ![]() .
.
(六)板书设计
| 8.2 椭圆的简单几何性质(五) |
||
|
一、直线与椭圆的位置关系 二、例题分析 例1 |
例2 例3 |
练习 小结 |