第五节 二次三项式的因式分解

扩展资料

代数恒等式的应用

湖北省浠水县实验中学（438200）  江思容

　　人教版初中代数第三册37页给出了一个代数恒等式：，其中是二次方程的两根，也是二次函数与x轴的两个交点的横坐标。下面介绍该代数恒等式在解题中的应用。

　　一、用于求方程中的参数值（或范围）

　　例1 若是方程的两实根，且，求k值。

　　解 ∵ 是已知方程的两实根，

　　

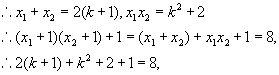
　　即，解之得。

　　经检验知，当时，原方程无实根，因此所求值应为。

　　例2 方程有一不大于－1，另一根不小于1，求m的取值范围。

　　解 设原方程的两根为，且，则有，取时，有。

　　∴  。　　①

　　再取，则有。

　　∴  。　　②

　　综①、②，知。

　　二、用于判断方程根的大小

　　例3  已知，且二次方程的根都是整数，试求方程最大的根。

　　解  不妨设方程两整数根为，且，则有。

　　取，有。

　　又∵  均为整数，且，，而题目要求的是最大根，故必有为所求。

　　三、用于求作新方程

　　例4  已知二次方程的两个根为，求以为两根的二次方程。

　　解  ∵  是原方程的根，

　　∴  ①

　　令，得

　　②

　　①×②得

　　。

　　令，得

　　③

　　方程③表明以为两根的方程是。

　　注：该题常见的解法是用韦达定理。

　　四、用于求二次函数解析式中的参数值

　　例5  已知二次函数和的图象都经过x轴上两个不同的点M、N，求a、b的值。

　　解  设两交点的坐标为，且，则有

　　①

　　②

　　①＋②，得③

　　根据已知条件，由③可得方程组

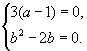　　解得或

　　经检验，知与相矛盾，故所求a，b的值是。

　　五、用于求二次函数的解析式

　　例6  如图，设二次函数的图象与x轴交于A、B两点，与y轴交于C点，若，求这个二次函数的解析式。

　　解在Rt中，，所以，又，所以即

　　，所以C点的坐标为（0，12）。

　　在Rt中，，

　　在Rt 中，。

　　所以A、B两点坐标分别为。

　　∵－16，9是方程的二根，故设。

　　又∵ 抛物线过C点，

　　∴

　　即。故所求二次函数的解析式为

　　。

返回页首