 设为首页
设为首页
 加入收藏
加入收藏
例1.设某个等差数列共有12项,其中奇数项的和为78,偶数项的和为96,求这个数列的后五项的和.
分析:数列的后五项是一个等差数列,其首项为原数列的第八项,公差就是原数列的公差,所以应先求原数列的首项与公差.
解:设等差数列为 ![]() ,其首项为
,其首项为 ![]() ,公差为
,公差为 ![]() ,奇数项构成以
,奇数项构成以 ![]() 为首项,
为首项, ![]() 为公差的等差数列,偶数项构成以
为公差的等差数列,偶数项构成以 ![]() 为首项,
为首项, ![]() 为公差的等差数列,于是有
为公差的等差数列,于是有 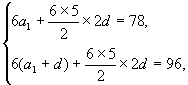 化简得
化简得 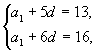 解得
解得 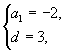 故
故 ![]() 所以
所以 ![]()
![]()
![]() .即这个等差数列后五项的和为125.
.即这个等差数列后五项的和为125.
说明:在运用等差数列前 ![]() 项和公式时依然要运用基本量的思想,把已知与所求都用基本量来表示,从而使题设与结论之间的关系明朗化.
项和公式时依然要运用基本量的思想,把已知与所求都用基本量来表示,从而使题设与结论之间的关系明朗化.
例2.等差数列
![]() 和
和 ![]() 的前
的前 ![]() 项和分别为
项和分别为 ![]() 和
和 ![]() ,若对一切正整数
,若对一切正整数 ![]() 都有
都有 ![]() ,求
,求 ![]() 的值.
的值.
分析: 由 ![]() 、
、 ![]() 的通项公式可求得
的通项公式可求得 ![]() 、
、 ![]() 的通项公式.
的通项公式.
解法一:令 ![]()
![]() ,则当
,则当 ![]() 时,有
时,有 ![]()
![]() ,所以
,所以 ![]()
解法二: ![]()
![]()
![]()
![]()
![]()
![]()
说明: 等差数列前 ![]() 项和
项和 ![]()
![]() ,当公差
,当公差 ![]() 时,
时, ![]() 是
是 ![]() 的二次函数,且常数项为0,所以等差数列前
的二次函数,且常数项为0,所以等差数列前 ![]() 项和
项和 ![]() 的一般形式是
的一般形式是 ![]() ,解法一就运用了这个形式;解法二则侧重等差数列前
,解法一就运用了这个形式;解法二则侧重等差数列前
![]() 项和公式的另一形式
项和公式的另一形式 ![]() ,是等差数列性质的应用.
,是等差数列性质的应用.
例3.把正整数以下列方法分组:(1),(2,3),(4,5,6),…,其中每组都比它的前一组多一个数,设
![]() 表示第
表示第 ![]() 组中所有各数的和,那么
组中所有各数的和,那么 ![]() 等于(
).
等于(
).
(A)1113 (B)4641 (C)5082 (D)53361
分析:第21组共有21个数,构成一个等差数列,公差为1,首项比第20组的最后一个数大1,所以先求前20组一共有多少个数.
解:因为第 ![]() 组有
组有 ![]() 个数,所以前20组一共有
个数,所以前20组一共有 ![]() 个数,于是第21组的第一个数为211,这组一共有21个数,
个数,于是第21组的第一个数为211,这组一共有21个数,
![]()
![]()
![]() ,故选
,故选 ![]() .
.
说明:认真分析条件,转化为数列的基本问题.
例4. ![]() 是等差数列
是等差数列 ![]() 的前
的前 ![]() 项和,
项和, ![]() ,且
,且 ![]() ,
, ![]() .求数列
.求数列 ![]() 的前
的前 ![]() 项和
项和 ![]() 的通项公式.
的通项公式.
分析:因为 ![]() ,所以应确定
,所以应确定 ![]() 的首项及公差.
的首项及公差.
解:设 ![]() 的首项为
的首项为 ![]() ,公差为
,公差为 ![]() ,则
,则 ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,由已知得
,由已知得 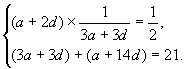 解得
解得 ![]() 所以
所以 ![]() ,
, ![]() ,
, ![]() ,
,
![]()
![]()
![]()
![]() .
.
说明:本题中的条件较多,通过分析找出基本量,简化条件,同时明确解题方向.
求数列 ![]() 的前
的前 ![]() 项和
项和 ![]() 使用的是裂项法,在第一节中曾经提到,在此复习为今后求极限作准备.
使用的是裂项法,在第一节中曾经提到,在此复习为今后求极限作准备.
例5.设等差数列
![]() 的前
的前 ![]() 项和为
项和为 ![]() ,已知
,已知 ![]()
![]()
(1)求公差 ![]() 的取值范围;
的取值范围;
(2)指出 ![]() 中哪一个值最大,并说明理由.
中哪一个值最大,并说明理由.
分析:求 ![]() 的取值范围应设法建立关于
的取值范围应设法建立关于 ![]() 的不等式(组);找
的不等式(组);找 ![]() 中的最大值可根据
中的最大值可根据 ![]() 的函数式用函数方法解决,也可根据数列的项的变化情况来定.
的函数式用函数方法解决,也可根据数列的项的变化情况来定.
解(1): ![]() 的首项为
的首项为 ![]() ,由已知有
,由已知有 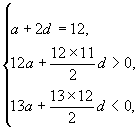 将
将 ![]() 代入后两个不等式,消去
代入后两个不等式,消去 ![]() 得
得 ![]()
![]() .
.
(2)解法一:由 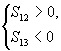
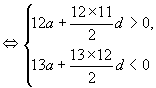
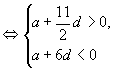
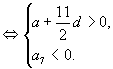 因为
因为 ![]() ,则
,则 ![]() ,可知
,可知 ![]() ,所以
,所以 ![]() 中最大的是
中最大的是 ![]() .(另法:
.(另法: ![]() ,得
,得 ![]() 所以
所以 ![]() 所以
所以 ![]() 最大.)
最大.)
解法二: ![]() ,二次函数
,二次函数 ![]() 的对称轴方程为
的对称轴方程为 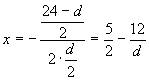 ,由于
,由于 ![]() ,有
,有 ![]() ,所以当
,所以当 ![]() 时,
时, ![]() 最大.
最大.
说明:根据项的值判断前 ![]() 项和的最值有以下结论:
项和的最值有以下结论:
①当 ![]() 时,
时, ![]() ,则
,则 ![]() 最小;
最小;
②当 ![]() 时,
时, ![]() ,则
,则 ![]() 最大;
最大;
③当 ![]() 时,
时, ![]() ,则
,则 ![]() 最小;
最小;
④当 ![]() 时,
时, ![]() ,则
,则 ![]() 最大.
最大.