第四节 反函数

　　例1 给出下列函数:

　　(1) ;   (2) ; 

　　(3) ;　　(4) ;

　  (5) .

　　其中不存在反函数的是__________________.

　　分析:判断一个函数是否有反函数,从概念上讲即看对函数值域内任意一个 ,依照这函数的对应法则,自变量 总有唯一确定的值与之对应,由于这种判断难度较大,故通常对给出的函数的图象进行观察,断定是否具有反函数.

　　解: (1) ,(2)都没有问题,对于(3)当 时, 和 ,且 .

　　对于(4) 时, 和 .对于(5)当 时, 和 .

　　故(3),(4),(5)均不存在反函数.

　　说明:从图象上观察,只要看在相应的区间内是否单调即可.

　　例2　求下列函数的反函数:

　　 (1)   ; (2)    ;

　　(3) .

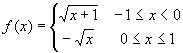　　分析:求反函数时,通常先由给定的解析式 中解出 ,再求出原来的函数的值域,再把 与 互换.

　　解: (1)由 得 ,又 得值域是 .

      .

　　(2)由 变形得 .

　　又 得值域是 ,

　　

　　(3)由 得 ; 由 得 .

 　　又 ( 的值域是 ,而 的值域是 ,

　　 .

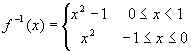　　说明:在求解方程时,一定要注意题目中对 的限制条件的使用,分段函数存在反函数时,也应分段求解它的反函数,一般情况下,它的反函数仍然是个分段函数.

　　例3　已知函数 ,求 的值.

　　分析: 符号 的意义即反函数 在 时的值,故可先求 ,再求 的值,但如果真正搞清了反函数与原来函数的关系,就会知道它的另一层含义即当原来函数的函数值为4时相应的自变量的取值.

　　解: 令 ,解此方程得 ,再考虑到 ,故 .

　　说明:此题意在要求学生不仅能在定义中理解互为反函数的两个函数之间的关系,还能从符号角度认识它们之间的关系,也正是基于这种理解才找到了更为简捷的方法.(此法对于求反函数比较复杂的题目尤为适用)

　　例4　已知函数 与其反函数 是同一个一次函数 ,试指出 的所有取值可能.

　　分析:此题可以有两种求解思路:一是求解 的反函数的解析式,与 比较,让对应系数相等,列出关于 的方程,二是利用两个函数图象的对称性,找对称点,利用点的坐标满足解析式来列方程.

　　解：由 知点 在图象上,则点 定在 的图象上,

　　于是          (1)

　　又 过点 ,则点 也在 的图象上,

　　于是     (2)

　　由(1)得 或 ,当 时,代入(2),此时(2)恒成立即 ;

　　当 代入(2)解得 .

　　综上, 的所有取值可能有 或 .

　　说明:此题是反函数概念与方程思想的综合.在这个题目中特殊点的选取一般是考虑计算简单方便,而且这种取特殊点列方程的方法在其他地方也有应用,故对此种方法要引起重视.另外此题在最后作答时,要求写出 的所有取值可能即要把 的取值与 的取值搭配在一起,所以解方程组时要特别小心这一点.

　　例5.已知函数 , ,求 的反函数.

　　分析: 由于已知是 ,所求是 的反函数,因此应首先由 找到 ,再由 求出 的表达式,再求反函数.

　　解:令 ,则 , , ,

    .于是有 .

　　由 得 ,由于 ,

 　　 .

　　又 , 的值域是 ,

　　 的反函数是 .

　　说明:此题涉及对抽象函数符号的认识与理解,特别是在换元过程中,相应变量的取值范围也要随之发生改变,这一点是学生经常忽略的问题.

　　例6.设定义域和值域都是 的函数 的反函数为 ,且对于任意 都有 ,

　　求证: 对任意 也成立.

　　分析:由函数 的性质推证其反函数的性质,应首先要把 的问题转化成 的问题,转化的依据是对互为反函数的两个函数关系的理解.

　　证明:令 ,其中 ,那么 .

　　则有       (1)

　　由于 对任意 成立,

　　 .由于 ,则 .

　　故有 ,即 .

　　说明:使用抽象函数符号进行简单的证明,是提高研究函数性质理论层次的一种要求,对于较好的学生应适当做一些这样的题目.