第五节 二次三项式的因式分解

典型例题

　　例1 在实数范围内分解因式：

　　（1）；

　　（2）.

　　分析  对于二次三项式的因式分解，如果在有理数范围内不能分解，一般情况要用求根公式，这种方法首先令=0，求出两根，再写成=.

　　解 （1）∵ 方程的根是

　　

　　∴

　　∴

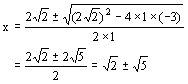
　　（2） ∵ 方程的根是

　　

　　∴

　　∴

　　

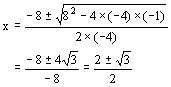
　　说明 分解结果是否把二次项系数乘进括号内，取决于能否把括号内的分母化去.

　　例2 把分解因式.

　　分析 此二次三项式中有两个字母和，在分解时可以把它看作是其中一个字母（如）的二次三项式，而另一个字母（）可看作是已知数.

　　解 ∵ 关于的方程的根是

　　

　　

　　，

　　∴

　　∴

　　说明 分解的结果不要丢掉两个一次因式里的.

　　例3当取何值时，二次三项式（1）在实数范围内能分解？（2）不能分解？（3）能分解成一个完全平方式？这个完全平方式是什么？

　　分析 二次三项式能否分解的关键是对应的二次方程是否有解，而方程是否有解由其的符号决定.

　　解 设

　　则

　　若，即时方程有两个不相等的实数根.

　　此时在实数范围内能分解.

　　（2）当时，不能分解.

　　（3）当时，方程为.

　　.

　　此时为一个完全平方式.

返回页首