第二节 函数

关于复合函数

　　高中数学对函数的研究主要类型有常见函数(七类)，由上述常见函数构成的复合函数，由常见函数做四则运算而得到的函数及实际生产生活中产生的函数．其中重点是前两类．常见函数在课本中都将系统研究，而复合函数在课本中没有给出定义，所以在这里我们对复合函数做点介绍．

　　一般来说，如果 是 的函数，而 又是 的函数，即 ，那么 关于 的函数 叫做 和 的复合函数．，其中 叫做中间变量．

　　在复合函数 中，自变量是 ， 是中间变量，因变量是 ， 是通过中间变量与自变量 间接建立起函数关系的．如 就可以看作反比例函数 与二次函数 复合而成，如果给出函数 ， ，它们就可以复合成一个以 为自变量 为因变量的函数关系即 ．在刚才形成这个复合函数的函数关系的过程实际上就是一个换元的过程，而且处理复合函数的很多问题都需要用换元法去处理．有了复合函数的概念，下列问题我们就都可以解决了．

　　1．已知函数 求 ．

　　2．已知函数 的定义域为 ，求 的定义域．

　　3．已知函数 ，求 ．

函数史话

　　设A、B是两个集合，如果按照某种对应法则 ，对于集合A中任何一个元素，在集合B中都有惟一的元素和它对应，这样的对应叫做从集合A到集合B的映射，记作 当集合A，B都是非空的数的集合，且B的每一个元素都有原象时，这样的映射 就叫定义域A到值域B上的函数．

　　笛卡儿引入变量后，随之而来的便是函数的概念．他指出y和 是变量（“未知量和未定的量”）的时候，也注意到y依赖于而变 ．这正是函数思想的萌芽．但是他没有使用“函数”这个词．

　　“函数”这个词用作数学的术语，最早是莱布尼茨，但其含义和现在不同，他指的是关于曲线上某点的一些线段的长（如横坐标、纵坐标、弦、切线、法线等）．

　　1718年，瑞士数学家约翰·贝努利给出函数的一个定义，同时第一次使用了“变量”这个词．他写道“变量的函数就是变量和变量以任何方式组成的量．”

　　“函数”这个概念随着数学的不断发展而变化．历史上每个阶段，都有它相应的定义．

　　18世纪，欧拉曾经前后给出函数的三种定义：

　　1．将函数定义为“解析表示式”他写道：“变量的函数是一个解析表达式，它是由这个变量和一些常量以任何方式组成的．”

　　2．将函数定义为“由曲线确定的关系”：“在 平面上徒手画出来的曲线所表示的y与 之间的关系．”

　　3．将函数定义为“变量之间的依赖变化”．他说：“如果某些变量，以这样一种方式依赖于另一些变量，即当后面这些变量变化时，前面这些变量也随之而变化，则前面的变量称为后面变量的函数．”

　　用现代的眼光去看，这三种定义都有一定的局限性．第1种、第3种两种定义容易理解，所以现在仍然被一些通俗的读物所采用，缺点在于过分狭窄，因为许多函数是没有解析表达式的，也有些函数并不随自变量 的变化而变化．第2个定义意义不够明确且局限于表达方式．不管怎样，欧拉定义对后世的影响很大．

　　1837年，德国数学家秋里赫勒进一步给出函数的定义：“对于在某区间上的每一个确定的 值，y都有一个或多个确定的值，那么y叫做 的函数．”这已经相当接近现在许多教科书所采用的定义．

　　19世纪70年代，康托的集合论出现之后，函数便明确地定义为集合间的对应关系．这是目前一般教科书所用的“集合对应”定义．

　　采用“集合对应”定义以后，摆脱了“变量”一词．

　　“变量”一词的意义至今尚不清楚．“自变量”这个提法本身也是有缺点的，因为变量必定依赖于时间而变，也就是它必定是时间的函数，不可能脱离时间而“自变量”．对于函数采用了“集合对应”定义以后，摆脱了“变量”与“自变量”等名词，定义函数无需再依赖于时间了．而变量这个词．许多学者主张废弃不用，有人主张将“自变量”“因变量”改为“第一值”“第二值”．

　　我国“函数”一词，是《代微积拾级》中首先使用的，这本书把函数定义为：“凡此变数中含彼变数，则此为彼之函数．”这里“函”是包含的意思．这定义大致相当于欧拉的解析表达式定义，在一个式子中“包含”着变量 ，那么这个式子就是 的函数．

　　函数这个概念已成为数学中最重要的几个概念之一，而变量这个词却逐渐被新的词所代替．

（2）函数值域的两种基本求解方法

　　由函数值域的定义，函数值的集合叫做函数的值域，因此函数的值域可由定义域直接推算．例如： 的值域为 ， 中，因为 为大于等于1的一切实数，所以 ，即函数的值域为

　　另一方面我们可以从方程的角度理解函数的值域，如果我们将函数 看做是关于自变量 的方程， 在值域中任取一个值 ， 对应的自变量 一定为方程 在定义域中的一个解，即方程 在定义域内有解；另一方面若 取某值 ，方程 在定义域内有解 ，则 一定为 对应的函数值．从方程的角度，函数的值域即为使关于 的方程 在定义域内有解的 的取值范围，如 变形得 ，方程在定义域 内有解的条件为 ， 即为函数的值域．

　　基于上述对函数值域概念的理解，求函数值域问题可通过直接推算和方程讨论两种方法解决．

　　例1 求函数 的值域．

　　分析：此题是关于 的一次分式函数，这种题目可通过求关于 的方程在定义域内有解的条件来求得值域，也可以经过变形（分离常量），观察得出结果．

　　解法1：把函数看成是 的方程，变形得 （ ），进一步整理得

方程在定义域 内有解的条件即为：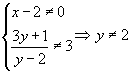

　　∴ 所求的值域为 ．

　　解法2：将原函数变形为

　　∵

　　∴

　　∴ ，即函数值域为 ．

　　例2 求函数 的值域．

　　解：易得函数的定义域为R．

　　由函数解析式：

　　当 时，方程 ．在定义域R内无解．

　　∴

　　当 时，有

　　∵ ，所以当且仅当 时 有实数解．

　　∴

　　综上所述，函数的值域是

　　例3 对于定义域为实数集R的函数 （ 为常数），回答下列下列问题：

　　（1）若 则            ；

　　（2）当 取由（1）所确定的值时，求 的值域．

　　解：（1）由 得 ，∴

　　（2）当 时，所给函数变为 定义域为R

　　由解析式得：

　　当 时， ∴ 属于函数的值域．

　　当 时，若方程有实数解，则

 ，

　　解得： （ ）．

　　故函数 的值域为

　　直接推算的方法要注意对函数式的化简，方程讨论的方法要在定义域内进行．

返回