设为首页
设为首页
 加入收藏
加入收藏
扩展资料
一次函数的图象是一条直线,限于初中学生的接受能力没有讲授曲线与方程的相应知识。这部分知识到高中还要学习,战线方程的知识高中也要继续学习。相应的资料可从高中教材中查到。
这里介绍二元一次不等式的有关知识。二元一次不等式![]() 或
或![]() 的解,表示平面内直线
的解,表示平面内直线![]() 将平面划分成的两个不同区域。
将平面划分成的两个不同区域。
下面研究不等式![]() (A、B均不为零)的解的情况。
(A、B均不为零)的解的情况。
![]()
![]() 可变形为
可变形为
![]()
从图形中可以看出
(1) ![]() 表示直线
表示直线![]() 上方区域
上方区域
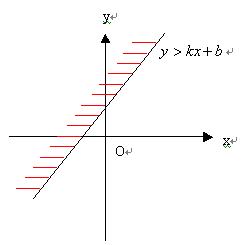
若k>0,![]() 表示直线
表示直线![]() 左上方区域;
左上方区域;
若k<0,![]() 表示直线
表示直线![]() 右上方区域;
右上方区域;
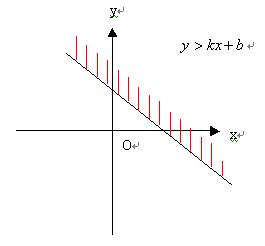
(2)![]() 表示直线
表示直线![]() 下方区域
下方区域
若k>0,![]() 表示直线
表示直线![]() 右下方区域;
右下方区域;
若k<0,![]() 表示直线
表示直线![]() 左下方区域;
左下方区域;
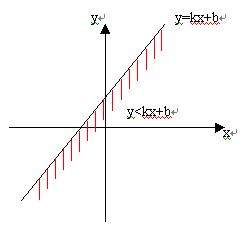
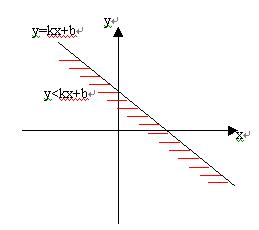
对于直线方程![]() ,若对于直线方程
,若对于直线方程![]() ,若A、B中有一个为零,则有x=m或y=n,于是可以看出:
,若A、B中有一个为零,则有x=m或y=n,于是可以看出:
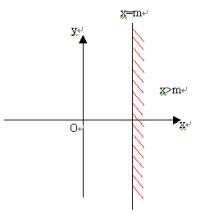
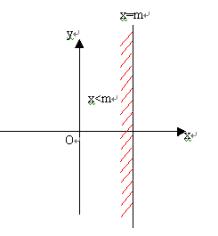
(1)x>m表示直线x=m右侧区域,而x<m表示直线x=m左侧区域
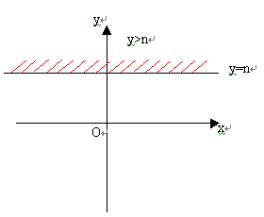
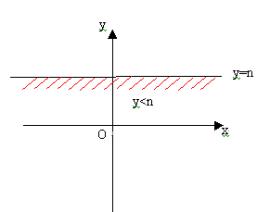
(2)y>n表示直线y=n上方区域,而y<n表示直线y=n下方区域
例1、图示下列不等式所表示的区域
(1)2x-y+1<0 (2)x-2y>0
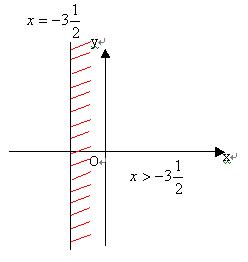
(3)![]() (4)2x+7>0
(4)2x+7>0
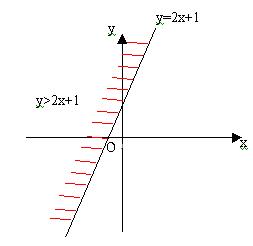
解:(1)2x-y+1<0即y>2x+1它表示直线y=2x+1的左上方区域;
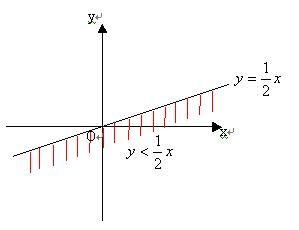
(2)x-2y>0即![]() ,它表示直线
,它表示直线![]() 右下方区域;
右下方区域;
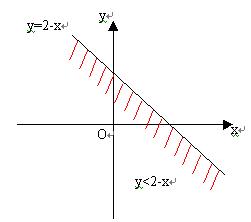
(3)![]() 即
即![]() ,它表示包括直线y=2-x和直线y=2-x左下方区域;
,它表示包括直线y=2-x和直线y=2-x左下方区域;
(4)2x+7>0即![]() ,它表示直线
,它表示直线![]() 右侧区域。
右侧区域。
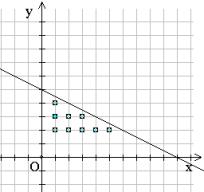
例2、欲购买1元和2元的笔若干支,并要求每种笔至少有2支,如果总钱数不超过10元,问有多少种买法?
解:设1元为x支,2元为y支,
由题意得![]()
它表示包括直线![]() 和直线
和直线![]() 左下方区域,而在该区域内,x、y都是不小于2的整数,这样的点的个数为9个,所以有9种买法。
左下方区域,而在该区域内,x、y都是不小于2的整数,这样的点的个数为9个,所以有9种买法。