第三节 函数的图象

扩展资料

　　在函数图象的教学中，教师需要澄清函数的图象、曲线与轨迹这三个不同的概念.

　　什么是曲线呢？欧几里得的《几何原本》中把曲线定义为“无宽度的长”或是“表面的边界”.这些虽也是曲线的本质属性，但它用到了尚未定义的“宽度”、“长”、“边界”等概念，所以不能作为曲线的定义.

　　在微积分中，常用参数方程

　　（其中为连续函数）来给出曲线，这虽然满足了许多用途的需要，但它包括的范围太广了，以至于产生了与人们常识抵触的现象，即以作此曲线的定义时，可以作出一条能填满边长为1的正方形的曲线，即皮亚诺曲线.

　　拓扑学中，把曲线定义为一维的连通闭集（此时，要求把抛物线那样的开曲线用一个无穷远点封闭起来），或与闭区间[a，b]同胚的点集，这样的定义既包含了通常意义下的曲线，又排除了“皮亚诺曲线”这种特例，当然，这一定义不能为中学声接受，但教师应掌握曲线这一科学定义，并用直观形象的语言指出曲线的真实含义.

　　函数 的图象是XOY平面上的有序数对（x，y）的集合

　　

　　这个点集可能是一条曲线，也可能不是一条曲线.例如 的图象就是一条曲线，而棉值为50分的邮票，如果买x张，那么应付金额 这是一个函数，其图象为

　　

　　是一些离散点集（1，50），（2，100），……，（x，50x），…的集合.而不是一条曲线.根据函数图象的定义，每一函数都应有它的图象.如狄里克雷函数

　　

　　也应有图象

　　这个图象在坐标平面上不好画出来，而且也不是曲线，但不能因此而说它没有图象.

　　由于中学教材的安排，学生最初看到的函数图象多是直线或曲线，到了高中，教材中指出函数图象可以是一些点或几条线段，教参中指出函数图象不一定是曲线，但没引起足够的重视，没有充分的理解.

　　不能以为轨迹就是曲线，也不能认为轨迹必是函数的某个函数的图象.在一般情况下，满足方程 的轨迹是各种各样的，不一定都是（平面）曲线或函数图象.如下面三个集合：

　　

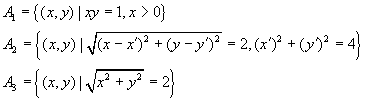
　　表示三个轨迹，但它们有不同的情况：集合 表示函数 的图象，也表示平面曲线；集合 则表示到圆周曲线 上各点距离为2的点的轨迹.此轨迹是一个点（0，0）.不是曲线；集合 表示曲线，但不是函数的图象.

　　因此函数的图象，曲线，轨迹是三个不同的概念，不能混淆.

　　参考文献：《数学思想方法与中学数学》   钱佩玲  邵光华编著     北师大出版社

返回页首