 设为首页
设为首页
 加入收藏
加入收藏
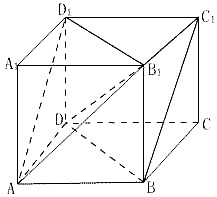
例1:已知正方体 ![]() .
.
求证:平面 ![]() 平面
平面 ![]() .
. 
证明:∵ ![]() 为正方体,
为正方体,
∴ ![]() ,
,
又 ![]() 平面
平面 ![]() ,
,
故 ![]() 平面
平面 ![]() .
.
同理 ![]() 平面
平面 ![]() .
.
又 ![]() ,
,
∴ 平面 ![]() 平面
平面 ![]() .
.
说明:上述证明是根据判定定理1实现的.本题也可根据判定定理2证明,只需连接
![]() 即可,此法还可以求出这两个平行平面的距离.
即可,此法还可以求出这两个平行平面的距离.
例2:如图,已知 ![]() ,
, ![]() ,
, ![]()
![]() .
.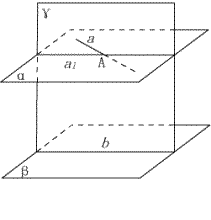
求证: ![]() .
.
证明:过直线 ![]() 作一平面
作一平面 ![]() ,设
,设 ![]() ,
, ![]() .
.
∵ ![]() ∴
∴ ![]()
又 ![]() ∴
∴ ![]()
在同一个平面 ![]() 内过同一点
内过同一点 ![]() 有两条直线
有两条直线 ![]() 与直线
与直线 ![]() 平行
平行
∴ ![]() 与
与 ![]() 重合,即
重合,即 ![]() .
.
说明:本题也可以用反证法进行证明.
例3:如果一条直线与两个平行平面中的一个相交,那么它和另一个也相交.
已知:如图, ![]() ,
, ![]() .求证:
.求证: ![]() 与
与 ![]() 相交.
相交.
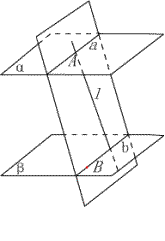 证明:在
证明:在
![]() 上取一点
上取一点 ![]() ,过
,过 ![]() 和
和 ![]() 作平面
作平面 ![]() ,由于
,由于 ![]() 与α有公共点
与α有公共点 ![]() ,
, ![]() 与
与 ![]() 有公共点
有公共点 ![]() .
.
∴ ![]() 与
与 ![]() 、
、 ![]() 都相交.
都相交.
设 ![]() ,
, ![]() .
.
∵ ![]()
∴ ![]()
又 ![]() 、
、 ![]() 、
、 ![]() 都在平面
都在平面 ![]() 内,且
内,且 ![]() 和
和 ![]() 交于
交于 ![]() .
.
∵ ![]() 与
与 ![]() 相交.
相交.
所以 ![]() 与
与 ![]() 相交.
相交.
例4:已知平面 ![]() ,
, ![]() ,
, ![]() 为夹在
为夹在 ![]() ,
, ![]() 间的异面线段,
间的异面线段, ![]() 、
、 ![]() 分别为
分别为 ![]() 、
、 ![]()
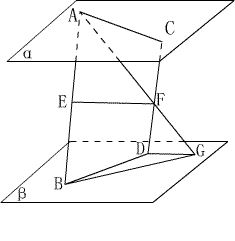 的中点.
的中点.
求证: ![]() ,
, ![]() .
.
证明:连接 ![]() 并延长交
并延长交 ![]() 于
于 ![]() .
.
∵ ![]()
∴ ![]() ,
, ![]() 确定平面
确定平面 ![]() ,且
,且 ![]() ,
, ![]() .
.
∵ ![]() ,所以
,所以 ![]() ,
,
∴ ![]() ,
,
又 ![]() ,
, ![]() ,
,
∴ △ ![]() ≌△
≌△ ![]() .
.
∴ ![]() .
.
又 ![]() ,
,
∴ ![]() ,
, ![]() .
.
故 ![]() .
.
同理 ![]()
说明:本题还有其它证法,要点是对异面直线的处理.
例5:如图,已知 ![]() 为△
为△ ![]() 所在平面外一点,
所在平面外一点, ![]() 、
、 ![]() 、
、 ![]() 分别是△
分别是△ ![]() 、△
、△ ![]() 、△
、△ ![]() 的重心.
的重心.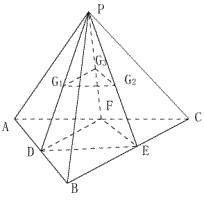
求证:平面 ![]() 平面
平面 ![]() .
.
分析:本题的思路在于如何找到三点 ![]() 、
、 ![]() 、
、 ![]() 或它们的三边与平面
或它们的三边与平面 ![]() 的关系.根据重心的性质易知应该连接
的关系.根据重心的性质易知应该连接 ![]() 、
、 ![]() 、
、 ![]() ,再根据相似比可知△
,再根据相似比可知△ ![]() 的三边分别与△
的三边分别与△ ![]() 的三边平行,进而可得结论.
的三边平行,进而可得结论.
例6:如图,已知矩形 ![]() 的四个顶点在平面上的射影分别为
的四个顶点在平面上的射影分别为 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() ,且
,且 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 互不重合,也无三点共线.
互不重合,也无三点共线.
求证:四边形 ![]() 是平行四边形.
是平行四边形.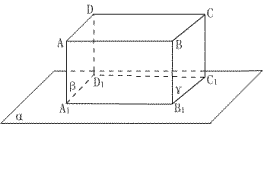
证明:∵ ![]() ,
, ![]()
∴ ![]()
不妨设 ![]() 和
和 ![]() 确定平面
确定平面 ![]() .
.
同理 ![]() 和
和 ![]() 确定平面
确定平面 ![]() .
.
又 ![]() ,且
,且 ![]()
∴ ![]()
同理 ![]()
又 ![]()
∴ ![]()
又 ![]() ,
, ![]()
∴ ![]() .
.
同理 ![]() .
.
∴四边形 ![]() 是平行四边形.
是平行四边形.