第三节 两条直线的位置关系

典型例题

　　例1 已知点 ， ，点 在坐标轴上，且 ，则满足条件的点 的个数是（  ）

  （A）1           （B）2              （C）3               （D）4

　　略解：点 在坐标轴上，可有两种情况，即在 轴或 轴上，点 的坐标可设为 或

　　由题意， ，直线 与直线 垂直，其斜率乘积为－1，可分别求得 或2， 或4，所以满足条件的点的坐标为（0，0），（2，0），（0，4）．

　　说明：①本题还可以有另外两种解法：一种是利用勾股定理，另一种是直角三角形斜边 与 轴交点 恰为斜边 中点，则由 到 、 距离相等的性质可解．②本题易错，可能只解一个坐标轴；可能解方程时漏解；也可能看到 、 各有两解而误以为有四点．

　　例2已知 的一个定点是 ， 、 的平分线分别是 ， ，求直线 的方程．

　　分析：利用角平分线的轴对称性质，求出 关于 ， 的对称点，它们显然在直线 上．

　　解： 关于 ， 的对称点分别是 和 ，且这两点都在直线 上，由两点式求得直线 方程为 ．

　　例3 求经过两条直线 和 的交点，并且垂直于直线 的直线的方程．

　　略解一：解得两直线 和 的交点为（ ， ），由已知垂直关系可求得所求直线的斜率为 ，进而所求直线方程为 ．

　　略解二：设所求直线方程为 ，将所求交点坐标（ ， ）代入方程得 ，所以所求直线方程为 ．

　　略解三：所求直线过点（ ， ），且与直线 垂直，所以，所求直线方程为

                       

　　即              ．

　　略解四：设所求直线得方程为

　　即                          （1）

　　由于该直线与已知直线 垂直

　　则             

　　解得                  

       代入（1）得所求直线方程为 ．

　　例4 在 中， 边上的高所在的直线的方程为 ， 的平分线所在直线的方程为 ，若点 的坐标为（1，2），求点 和点 的坐标．

　　解：解直线 和直线 的交点得 ，即 的坐标为 ，

　　∴                    ，

　　又∵ 轴为 的平分线，

　　∴                    

　　又∵直线 为 边上的高，由垂直得，

                          

　　设 的坐标为 ，则 ， ，

　　解得                     ， ，

即 的坐标为

　　例5 已知定点 （3，1），在直线 和 上分别求点 和点 ，使 的周长最短，并求出最短周长．

　　分析：由连接两点的线中，直线段最短，利用对称，把折线转化为直线，即转化为求两点间的距离．

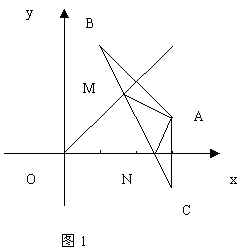
　　解：如图1，设点 关于直线 和 的对称点分别为 ，

　　∵

　　 又

　　周长最小值是：      

　　由两点式可得 方程为：

         

　　而且易求得： （ ， ）， （ ，0）

　　此时，周长最短，周长为

　　例6 已知实数 ， 满足 ，求证： ．

　　简解：本题的几何意义是：直线 上的点（ ， ）与定点 的距离的平方不小于 ．因为直线外一点与直线上任一点连线中，垂线段距离最短，而垂线段的长度即距离 ，

　　所以 ，即 ．

　　说明：本题应为不等式的题目，难度较大，证明方法也较多，但用解析几何的方法解决显得轻松简捷，深刻地体现了数形结合的思想．

　　例7 在平面直角坐标系中， ， ，点 在 上 ， ， ，试在 轴的正半周上求一点 ，使 取得最大值．

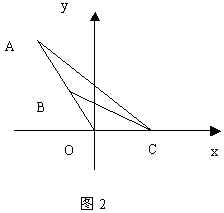　　分析：要使最大，只需最大，而是直线到直线的角（此处即为夹角），利用公式可以解决问题．

　　解：如图2，设点

　　∵ ， ， ，

　　∴ ，

 ，

　　于是直线 、 的斜率分别为：

 ，



　　∴ ＝

　　　　＝

　　　　＝

       　　＝

　　∵

　　∴

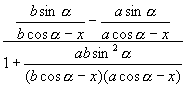
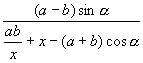
　　当且仅当 即 ， 点的坐标为（ ，0），由 可知 为锐角，所以此时 有最大值 ．

　　说明：本题综合性强，是三角、不等式和解析几何知识的交汇点．另外本题也是足球射门最大角问题的推广．

返回页首