 设为首页
设为首页
 加入收藏
加入收藏
例1 解不等式 ![]()
分析 解含有绝对值的不等式,通常是利用绝对值概念
![]() ,将不等式中的绝对符号去掉,转化成与之同解的不含绝对值的不等式(组),再去求解.去绝对值符号的关键是找零点(使绝对值等于零的那个数所对应的点),将数轴分成若干段,然后从左向右逐段讨论.
,将不等式中的绝对符号去掉,转化成与之同解的不含绝对值的不等式(组),再去求解.去绝对值符号的关键是找零点(使绝对值等于零的那个数所对应的点),将数轴分成若干段,然后从左向右逐段讨论.
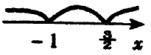
解 令
![]() ,∴
,∴
![]() ,令
,令 ![]() ,∴
,∴ ![]() ,如图所示.
,如图所示.
(1)当 ![]() 时原不等式化为
时原不等式化为 ![]()
∴ ![]() 与条件矛盾,无解.
与条件矛盾,无解.
(2)当 ![]() 时,原不等式化为
时,原不等式化为 ![]() .
.
∴ ![]() ,故
,故 ![]() .
.
(3)当 ![]() 时,原不等式化为
时,原不等式化为![]() .
.
∴ ![]() ,故
,故 ![]() .
.
综上,原不等式的解为 ![]() .
.
注意 找零点去绝对值符号最好画数轴,零点分段,然后从左向右逐段讨论,这样做条理分明、不重不漏.
例2 求使不等式 ![]() 有解的
有解的 ![]() 的取值范围.
的取值范围.
分析 此题若用讨论法,可以求解,但过程较繁;用绝对值的几何意义去求解十分简便.
解法一 将数轴分为
![]() 三个区间
三个区间
当 ![]() 时,原不等式变为
时,原不等式变为 ![]() 有解的条件为
有解的条件为 ![]() ,即
,即 ![]() ;
;
当 ![]() 时,得
时,得 ![]() ,即
,即 ![]() ;
;
当 ![]() 时,得
时,得 ![]() ,即
,即 ![]() ,有解的条件为
,有解的条件为 ![]() ∴
∴ ![]() .
.
以上三种情况中任一个均可满足题目要求,故求它们的并集,即仍为 ![]() .
.
![]()
解法二 设数
![]() ,3,4在数轴上对应的点分别为P,A,B,如图,由绝对值的几何定义,原不等式
,3,4在数轴上对应的点分别为P,A,B,如图,由绝对值的几何定义,原不等式 ![]() 的意义是P到A、B的距离之和小于
的意义是P到A、B的距离之和小于 ![]() .
.
因为 ![]() ,故数轴上任一点到A、B距离之和大于(等于1),即
,故数轴上任一点到A、B距离之和大于(等于1),即 ![]() ,故当
,故当 ![]() 时,
时, ![]() 有解.
有解.
例3 已知 ![]() ,求证
,求证 ![]() .
.
分析 根据条件凑
![]() .
.
证明 ![]()
![]() .
.
说明 这是为学习极限证明作的准备,要习惯用凑的方法.
例4 求证 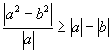
分析 使用分析法
证明 ∵
![]() ,∴只需证明
,∴只需证明 ![]() ,两边同除
,两边同除 ![]() ,即只需证明
,即只需证明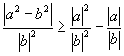 ,即
,即![]()
当 ![]() 时,
时, ![]() ;当
;当 ![]() 时,
时, ![]() ,原不等式显然成立.∴原不等式成立.
,原不等式显然成立.∴原不等式成立.
说明在绝对值不等式的证明,常用分析法.本例也可以一开始就用定理:
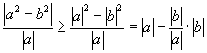
(1)如果 ![]() ,则
,则 ![]() ,原不等式显然成立.
,原不等式显然成立.
(2)如果 ![]() ,则
,则 ![]() ,利用不等式的传递性知
,利用不等式的传递性知 ![]() ,
, ![]() ,∴原不等式也成立.
,∴原不等式也成立.