第五节 等比数列前n项和

典型例题

　　例1.求和： .

　　分析：当 时， 是由数列 与数列 的相应的项相乘而来的，所以用错位相减法来求和.

　　解：当 时，

　　当 时， ，①

　　左右两边分别乘以 得：

　　 ，②

①、②相减得：

　　于是 .

　　说明：求和问题要分析数列的项的结构，当通项是一个等差数列与等比数列的乘积时，用错位相减法求和，此时要注意等比数列的公比是否为1（用字母表示公比时）.

　　例2.已知 是等比数列 的前 项和，且有 求 的值.

　　分析：由两个方程不能求出确定的 ，只能得到一个关系，所以应采用整体代入的方法.

　　解：设等比数列的首项为 ，公比为 ， 由 可知 ，故

 两式相除得 ，即 .

　　于是有



　　说明：本题强调的是基本量思想与整体思想，整体思想往往是设而不求，整体替换.

　　例3. 求数列 的24项的和.

　　分析： ，可用裂项法求和.

　　解：

　　　　　　 .

　　说明：裂项法是求和的重要方法之一，要把数列的每一项分裂为两项之差，求和时使得中间的大多数项互相抵消了.

　　例4　设 是由正数组成的等比数列， 是其前 项和.求证： .

　　分析：先比较 与 的大小，再根据对数函数的单调性得到所要证明的不等式.

　　证明：设等比数列 的首项为 ，公比为 .

　　当 时，

　　当 时，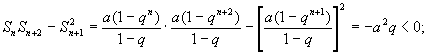

 ， ，

　　故有 .

　　说明：解题中注意等比数列前 项和公式要对公比进行分类；注意比较两数大小的基本方法是比较法，特别是作差比较法，还要注意结合函数的有关知识.

　　例5. 已知数列 中， 且当 时， .

　　（1）求 的通项公式；

　　（2）求证：

　　分析：该数列从第二项开始，每一项是其前面所有项之和，于是通项 与一个和有关，所以引入前 项和.

　　解：（1）设 ，

　　所以当 时有 ，同时又 ，两式相减得 ，于是 所以 是等比数列，公比为2.

　　因为 所以 ，故当 时， ,

　　所以

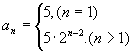
　　证明：（2）



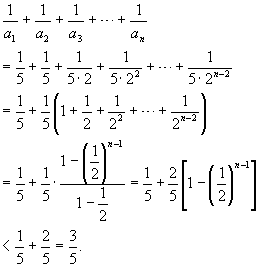
　　说明：在解题中注意项数的初始值，以及数列通项与和的相互转化.

返回页首