第一节 数列

典型例题

　　例1．数列 共有__________项．

　　分析：数一个数列的项数都是从1开始的，找项与项数的关系关键是找首项与1的关系．

　　解：已知数列的项数与数列 的项数相同，

　　又 ，所以又与数列 的项数相同．

　　因为 共有 个数，所以 共有 个数．

　　因此 有 个数．

　　说明：数清项数是解决数列问题的首要问题，在有穷数列中，数列的末项未必是数列的第 项，即有穷数列的项数未必是 ．一定要区分有穷数列的末项与通项．

　　例2．已知数列 中， ，对任意 ， ，都有 则 ______．

　　分析：已知条件 表示了无数个等式： ， ， ，再加上 这一条件便确定了这个数列，即可递推求出数列的各项．

　　解：令 ，得 ， ， ．

　　令 ，得 ，

 ．令 ，得

　　令 ，得

　　 ．

　　说明：本题涉及了方程的思想，同时体现了特殊与一般的关系．也可能有学生看出 就求出了数列的通项公式，用代入法便可求出数列的任意一项，如果希望学生看出这一结果，可将所求换成求项数较大的项．

　　例3．数列 的通项公式为 ， 表示数列 的前 项和，求 ．

　　分析：数列的每一项 ，数列的前 项和便抵消了一些项．

　　解：



 ．

　　说明：可以在此补充裂项求和法，当然裂项法不仅仅针对分式形式的通项公式，只要 的形式就行．

　　例4．在数列 中， ，那么这个数列中的最大项与最小项的项数为____________．

　　分析：通过函数 的取值情况来探求数列的最大项及最小项．

解：函数 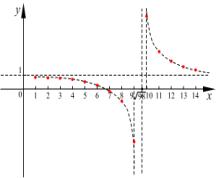，其图象是由函数 的图象向右平移 个单位，再向上平移1个单位得到， 根据图象可得 最小， 最大，即第9项最小，第10项最大．

　　说明：数列的项与项数构成特殊的函数关系，研究其最值的方法就是求函数最值的基本方法，求函数最值的方法之一是数形结合，即利用函数图象来判断最值．

　　例5．设数列 各项均为正数的数列， ，且满足： ， 则数列 的通项公式为____________．

　　分析：解决此问题有两个思路，一是求出数列的前几项，由此猜出数列的通项公式（因为这是填空题）；另一个思路是化简已知递推式（因式分解，降次），使 与 明确，简洁，便于寻求解决方式．

　　解：由已知得 ， ， ，

 ， ．

　　于是有 ，

　　这 个等式相乘得 ，由于 ，所以 ．

　　说明：这种方法叫做迭乘法，相类似的还有迭加法．