 设为首页
设为首页
 加入收藏
加入收藏
例1 判断下列各组的两个函数是否相同,并说明理由.
(1)
![]() 与
与 ![]() ;
;
(2)
![]() 与
与 ![]()
(3)
![]() 与
与 ![]() ;
;
(4)
![]() 与
与 ![]() ;
;
(5)
![]() 与
与 ![]() .
.
分析:判断两个函数是否相同,应着眼于两个函数的定义域和对应法则的比较,而求定义域时应让原始的解析式有意义,而不能进行任何非等价变换,对应法则的判断需判断它的本质是否相同而不是从表面形式上下结论.
解:(1)不同,因为它们定义域不同.
(2)不同,前者的定义域是 ![]() 或
或 ![]() ,后者的定义域是
,后者的定义域是 ![]() .
.
(3)相同,定义域均为非零实数,对应法则都是自变量取倒数后加1.
(4)不同,定义域是相同的,但对应法则不同.
(4)相同,将 ![]() 利用绝对值定义去掉绝对值结果就是
利用绝对值定义去掉绝对值结果就是 ![]() .
.
说明:此题的目的在于强化函数是三要素构成的整体,且三要素中值域是由定义域和对应法则共同确定的,判断时可以只考虑定义域和对应法则是否相同,同时提醒学生,认识函数对应法则必须认清它的本质,而不是从表面上做判断.
例2 已知集合 ![]() ,
, ![]() ,那么集合
,那么集合 ![]() 中所含元素个数为( ).
中所含元素个数为( ).
![]() 0
0
![]() 1
1
![]() 0或1
0或1
![]() 1或2
1或2
分析:此题是以集合语言表述的问题,解决问题的第一步在于集合语言的翻译与理解,然后结合函数概念在运动变化过程中进行研究,求解时,可以先从形的角度,再从数的角度提高认识.
解:从函数观点看,两个集合的交集中所包含的元素的个数,从数的角度即在 ![]()
![]() 中,令
中,令 ![]() ,看有几个相应的
,看有几个相应的 ![]() 与之对应;从形的角度即
与之对应;从形的角度即 ![]()
![]() 的图象与直线
的图象与直线 ![]() 有几个公共点,由于
有几个公共点,由于 ![]() 是不确定的,
是不确定的,
于是当 ![]()
![]() 时,有一个交点,当
时,有一个交点,当 ![]() 时,则没有交点,所以应选
时,则没有交点,所以应选 ![]() .
.
说明:此题目的在于进一步认识函数概念本质,纠正只注意对应法则而忽视定义域作用的毛病,而且还应从数和形两角度认识问题,解决问题.
例3 求下列函数的定义域,要求把结果写成区间形式.
(1)
![]() ;
;
![]() ;
;
(3)
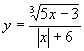 ; (4)
; (4) 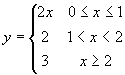 ;
;
(5)
![]() ;
(6)
;
(6) ![]() ,(
,( ![]() 为圆的半径)
为圆的半径)
分析:求定义域即使 ![]() 的解析式有意义,其中要注意有实际背景的问题和人为限制因素对定义域的影响.
的解析式有意义,其中要注意有实际背景的问题和人为限制因素对定义域的影响.
解:(1)使 ![]() 有意义应满足
有意义应满足 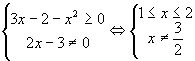 .
.
故函数的定义域为 ![]() .
.
(2)使 ![]() 有意义应满足
有意义应满足 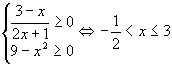 . 故函数定义域为
. 故函数定义域为
![]() .
.
(3)使 ![]() 有意义应满足
有意义应满足 ![]() .故函数定义域为
.故函数定义域为 ![]() .
.
(4)分段函数的定义域为 ![]() .
. ![]()
(5)由于 ![]() ,所以
,所以 ![]() 或
或 ![]() .
.
故定义域为 ![]() .
.
(6)从 ![]() 有意义的角度对
有意义的角度对 ![]() 没有限制,但由于
没有限制,但由于 ![]() 使圆的半径,应使非负数,故函数定义域为
使圆的半径,应使非负数,故函数定义域为 ![]() .
.
说明:此题的目的一方面掌握求定义域的基本方法,熟悉用区间表示集合,另一方面包含对分段函数定义域的认识及有人为限制的问题求定义域应注意的问题.
例4 画出下列函数的图象
(1)
![]() 且
且 ![]() ; (2)
; (2) ![]() ;
;
(3)
![]() ;
(4)
;
(4) 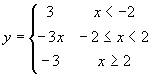 .
.
分析:对于常见函数由于其特征学生很熟悉,故一般只要选几个关键点,但要注意人为限制的定义域对图象的影响.对分段函数可先处理为若干段常见函数,在转折点的取舍上格外注意.
解:如图所示:
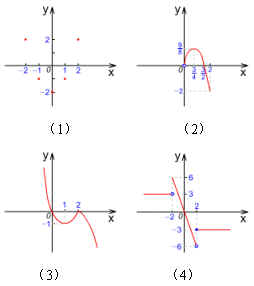
例5 某商场饮料促销,规定一次购买一箱在原价48元的基础上打9折,一次购买两箱可打8.5折,一次购买三箱可打8折,一次购买三箱以上均可享受7.5折的优惠.若此饮料只整箱销售且每人每次限购10箱,试用解析法写出顾客购买的箱数 ![]() 与所支付的费用
与所支付的费用 ![]() 之间的函数关系,并画出其图象.
之间的函数关系,并画出其图象.
分析:阅读理解题意是解此题的第一步,其次注意题目的限制条件对定义域的制约.
解:由题意可得, 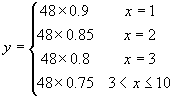 .如图:
.如图:
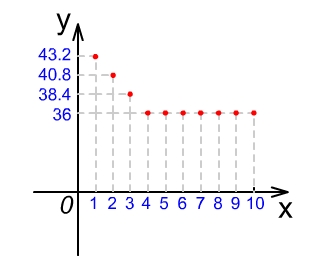
说明:一方面提高应用意识,另一方面体会函数图象的特点可以是一群孤立的点.
例6 若 ![]() 求
求 ![]() 的值.
的值.
分析:既然求 ![]() ,当然应在已知中令
,当然应在已知中令 ![]() 得
得 ![]() ,从方程的观点看,把
,从方程的观点看,把 ![]() 和
和 ![]() 都当作未知数而要求得
都当作未知数而要求得 ![]() 的值,还须再找出另一个
的值,还须再找出另一个 ![]() 与
与 ![]() 的方程.
的方程.
解:另 ![]() 得
得 ![]() ,另
,另 ![]() ,得
,得 ![]() .由此消去
.由此消去 ![]() ,解得
,解得 ![]() =1.
=1.
说明:把抽象函数记号与方程思想融与一体,深刻体会两者之间的关系是此题的主要目的.