第十九节 圆的周长、弧长

典型例题

　　例1、半径为4cm，50°的圆心角所对应的弧长是多少？

　　解：设弧长为lcm，∵n=50°，

　　R=4，∴l （cm）．

　　说明：弧长公式的简单应用．

　　例2、已知：弧长为l，它所对应的圆心角为120°，求这条弧所对应的弦长．

　　解：如图，∠AOB=120°， 的长=l，

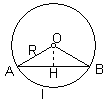　　则l ，∴R= l，

　　作OH⊥AB于H，在Rt△AOH中，∠A=30°，

　　∴AH=AO·cos30°= l，∴AB=2AH= l．

　　答：这条弧所对应的弦长为 l．

　　说明：（1）灵活应用弧长公式、解直角三角形、锐角三角函数；（2）弧长公式l 中三个变量l、n、R，知道其中任两个量，就可求出第三个量，其中n没有单位，是圆心角的度数，l与R的单位一致．

　　例3、某地工人为了用起重机吊起两条半径分别为10cm和30cm的钢管，需要先用钢丝绳把这两条钢管捆绑扎紧．问扎紧这两条钢管的钢丝绳至少要多长(打结部分不计，结果化简后可用π和根式表示)?

　　解： 设大、小管的轮廓线分别为⊙O_l和⊙O₂，如图所示．

　　依题意，两圆外切，设切点为P．两圆的外公切线与⊙O_l和⊙O₂分别切于A，B，E，F．连O_lA，O₂B，作O₂C⊥O_lA于点C，则

　　O_lC=O_lA-CA=O_lA-O₂B=20，O_lO₂=30+10=40．

　　在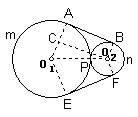Rt△O_lO₂C中，

　　  ．

　　 ∴AB= ．

　　 又 ，∴∠A O_lO₂=60°，∠AO_lE=120°．

　　 ∴ 的长= ．  的长= ．

　　 ∴钢丝的长=2AB+ 的长+ 的长=

　　 ∴扎紧这两条钢管的钢丝绳至少要 （cm）．

　　说明：本题综合应用圆与圆的有关知识．求公切线的长、弧长等知识．

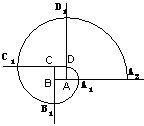
　　例4、（福州市，2002）如图：四边形ABCD是正方形，曲线DA_lB_lC_lD_l……叫做“正方形的渐开线”，其中 、 、 、 、…的圆心依次按A、B、C、D循环，它们依次连接．取AB=l，则曲线DA_lB_l…C₂D₂的长是______(结果保留π)．

　　分析： 的长= ， 的长= ， 的长= ， 的长= ，……

　　找出规律，可求．答案：18π．

　　说明：本题不仅应用弧长公式，更重要地是利用了归纳法．

返回页首