第六节 一元二次方程的应用

典型例题

　　例  把分解因式

　　解：∵  的根是

　　　

　　

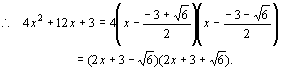
　　说明  把系数4拆成分别乘到两个括号中，将分解结果化简，这时注意不能把每个括号都乘以4.另外分数线有括号的作用，分数线前又是减号，去分母时注意符号的变化.

　　根据此题的特征，用配方法分解更为简单.即

　　

　　例  一个三位数、十位数字比百位数字大3，个位数字等于百位数字与十位数字的和.已知这个三位数比个位数字的平方的5倍大12，求这个三位数.

　　分析  题中的前一句话叙述了三位数中三个数字之间的关系，三个数字中以百位数字为中心，因此设百位数字为x较好，十位数字和个位数都可以用x的代数式表示，从而就有了三位数.抓住后一句话三位数＝个位数字这个等量关系，可以列出方程.

　　解：设百位数字为x，则十位数字为，个位数字为即.

　　依题意，有

　　整理后，得

　　∴，（不符合题意，舍去）.

　　当时，.

　　答：这个三位数是257.

　　说明  如果百位数字、十位数字、个位数字分别有a、b、c表示，则三位是，而不能写成abc.

　　例  某公司八月份售出电脑200台，十月份售出242台，这两个月平均每有增长的百分率是多少？

　　分析  设平均每月的增长率为x.那么九月份售出电脑台，即台，十月份售出台，即台，于是根据题意，可以列出方程.

　　解：设平均每月增长的百分率为x.

　　依题意，有

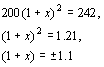
　　∴  （不符合题意，舍去）

　　答：平均每月增长的百分率为10%.

　　说明  在有关增长率的问题中，要掌握等量关系：，其中a为变化前的数，如本题中的200台，p为变化后的数，如本题中的242台，x为增长（降低）率，n为变化次数，如本题从八月到十月份共变化两次，因此.

　　例  学校要把校园内一块长50米，宽40米的长方形空地进行绿化.计划中间种花，四周留出宽度相同的地种草坪，且花坛面积占整个绿化地面积的，求草坪的宽度.

　　分析  设草坪的宽度是x米，那么花坛的长是（）米，宽是（）米.根据长方形的面积公式和题中的等量关系，花坛面积绿化地的面积，可列方程.

　　解：设草坪的宽度是x米.

　　依题意，有

　　整理后，得

　　∴（不符合题意，舍去），.

　　说明  要切实检验解方程所得的值是符合实际意义，不要误认为正数都符合题意，负数都不符合题意.如本题中若草坪宽度为35米，花坛将不存在，因此要舍去.

返回页首