第三节 一元二次方程的根的判别式

典型例题

　　例1 不解方程，判别下列方程的根的情况：

　　（1） ；
　　（2） ；
　　（3） .

　　分析  不解方程，要想判别方程的根的情况，只要把 求出即可判别.

　　解 （1）原方程可化为

　　
　　∵ ，
　　∴ ，
　　∴原方程有两个不相等的实数根；

　　（2）∵ ，
　　∴ ，
　　∴原方程没有实数根；
　　（3）原方程可化为
　　
　　∵ ，
　　∴ ，
　　∴原方程有两个相等的实数根.

　　说明：用根的判别式来判别根的情况，一定要把方程变形为一元二次方程的一般形式.

　　例2 若关于 的方程 有两个不相等的实数根，求 的取值范围.

　　分析  因为方程有两个不相等的实数根，所以方程是一元二次方程，因此， .

　　解 方程 有两个不相等的实数根的条件是

　　
　　解这个方程组，得
　　
　　所以， 的取值范围是 ，但 .

　　说明：解此类题目，一定要把满足题目的所有条件列成一个方程组，然后求方程组的解集.

　　例3  求证：当 和 的符号相反时，一元二次方程 一定有两个不相等的实数根.

　　分析 要想证明方程有两个不相等的实数根，须先写出 .

　　证明：在 中，当当 和 的符号相反时，有
　　 ，
　　又由于 为任何实数时，总有 ，
　　于是有    .
　　所以，当 和 的符号相反时，一元二次方程 一定有两个不相等的实数根.

　　说明：证明给出了一个命题，不必计算 的值，只要看一看 和 的符号是否相反即可.一般情况下， 为正值，只要 是负数，一元二次方程一定有不相等的实数根.反之不成立.

　　例4 （1）已知 、 、 是三角形的三边，判别方程 根的情况；

　　（2）若方程 没有实数根，判别方程 根的情况；

　　分析 两个方程的系数都含有字母，但字母人为地给出一定的条件，因此，是在特定的条件下，对“ ”的表达式进行分析，从而判别二次方程根的情况.解这类题要注意所给条件与“ ”表达式之间的沟通.

　　解 （1）
　　
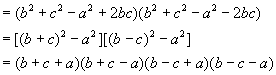
　　∵ 、 、 为三角形的三边
　　∴
　　∴
　　∴原方程无实数根.

　　（2） 方程 没有实数根的条件：

　　 ，即 ，
　　所以， .
　　对于方程 ，
　　
　　∵ ，∴ ，∴
　　∴方程 有两个不相等的实数根.

　　说明：求解这类问题，首先要由给出的条件，确定字母的取值范围或字母之间的关系，然后在这样的特定条件下，确定“ ”的符号，以判定根的情况.

　　例5 （1） 取何值时，关于 的方程 的有两个实数根？

　　（2）若关于 的一元二次方程 有两个不相等的实数根，求 的最大整数值.

　　解 （1） 关于 的方程 有两个实数根的条件是
　　
　　解方程组，得：
　　  .
　　所以，当 时，方程 的有两个实数根.

　　（2）方程 有两个不相等的实数根的条件是

　　
　　解方程组，得：
　　
　　∴
　　∴ 的最大整数值为0.

　　说明：一定不要忽略题目的隐含条件. 第（1）小题方程有两个实数根，一定为一元二次方程，所以一定有 .第（2）小题说方程是一元二次方程，一定有二次项系数不为零.

返回页首