第二节 平行线分线段成比例定理

典型例题

　　例1  如图所示， ，求BC的长.

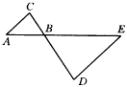
　　分析：要求BC，由于BC和BD是对应线段，因此只要得出 即可.

　　解：因为 ，

　　所以 .

　　所以 （平行于三角形一边的直线截其他两边的延长线所得的对应线段成比例）.

　　所以 .

　　所以 .

　　说明：在列比例式求某线段的长时，应尽可能将需求的线段写成比例式第一项，以减少比例变形，减少错误.

　　例2  如图所示， .

　　求证： .

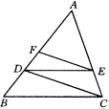
　　分析：要证 ，只要证 ，由于AF、AD、AB在同一直线上，因此上式不能直接用定理证，于是想到用过渡比.从基本图形A型中立即可找到过渡比为 .

　　证明：因为 ，

　　所以 （平行于三角形一边的直线截其他两边所得的对应线段成比例）.

　　因为 ，

　　所以 ，

　　所以 ，即

　　说明：等积式常常转化为比例式证明；要善于从复杂图形中识别出基本图形中的公共部分（即 ），它往往是构成证明中的过渡比.

　　例3  已知：如图所示，直线FD和 的BC边交于D，与AC边交于E，与BA的延长线交于F，且 ，求证： .

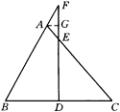　　 分析：本题只要证 即可.由于 与 没有直接联系，因此必须寻找过渡比将它们联系起来，因此考虑添加平行进行构造.

　　证明：过A作 ，交DF于G点.

　　因 ，

　　所以 .

　　又 ，所以 .

　　因为 ，所以 .

　　所以 ，

　　即 .

　　说明：本题过点A还有一种方式作平行线构造基本图形，过B、C都有两种方式作平行线，构造基本图形.

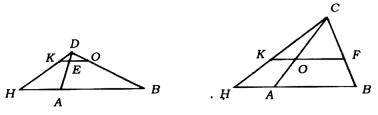
　　例4 如下图， 中，D是BC的中点，M是AD上一点，BM、CM的延长线分别交AC、AB于F、E.

　　求证： .

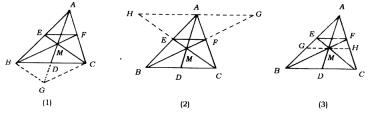
　　分析  要证明 ，想通过角之间的关系达到目的显然是不可能的，而要利用成比例线段判定两直线平行的判定定理，图中又没有平等条件，因此要设法作出平行线，以便利用判定定理.如何作出平行线，要充分考虑到中点D条件的应用.

　　分析一 延长AD至G，使DG=MD，连结BG、CG如上图（1），则四边形BGCM为平行四边形，可以立即将 、 转化成中间比 .

　　解法一 延长AD至G，使 ，连结BG、CG.

　　∵

　　∴四边形 为平行四边形.

　　∴

　　∴

　　∴ ，

　　∴

　　分析二 过A作BC的平行线，与BF、CE的延长线分别交于G、H（如上图（2）），则

　　

　　要证明 ，只要证 ，这是不难解决的.

　　解法二 过A作BC的平行线，与BF、CE的延长线分别交于G、H.

　　

　　∴ ，

　　∴

　　

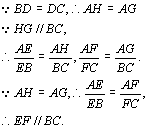
　　分析三 过M作BC的平行线，分别与AB、AC交于G、H，∵ ， .要证 ，只要证 ，这可以通过中间比立即证得.

　　证法三 过M作BC的平行线，分别与AB、AC交于G、H.

　　则

　　

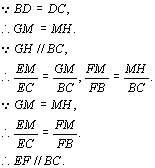
　　例5 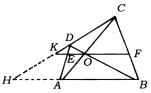如图，四边形ABCD中，AC、BD交于O，过O作AB的平行线，与AD、BC分别次于E、F，与CD的延长线交于K.求证： .

　　分析  KO、KE、KF在一条直线上，要证明 ，即要证 ，显然要寻找中间比，现有图形无法将线段KO、KE、KF与平行线分线段成比例定理及其推论联系起来，若延长CK、BA，设它们交于H，则图形中出现如上题所说的两个基本图形.

　　这就不难将 、 ，进行转换而找到中间比.

　　证明 延长CK、BA，设它们交于H，

　　

　　∴

　　 同理可得

　　　　

　　∴

　　即

　　说明（1）本题所作的辅助线，不仅构造了两个常见的基本图形，而且可以直接利用三角形一边的平行线的性质定理，找到 与 的中间比，使问题得以突破.

　　（2）可以由两个基本图形直接得到

　　

返回页首