 设为首页
设为首页
 加入收藏
加入收藏
教学设计示例一
9.7 棱 柱 第一课时
教学目标:理解棱柱的概念、分类;掌握棱柱的性质.
教具准备:投影胶片、多媒体课件.
教学过程:
[设置情境]
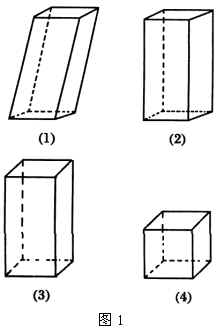
教师拿几个模型(如图1)一一呈现出来让同学们观察,并讨论哪些是棱柱.
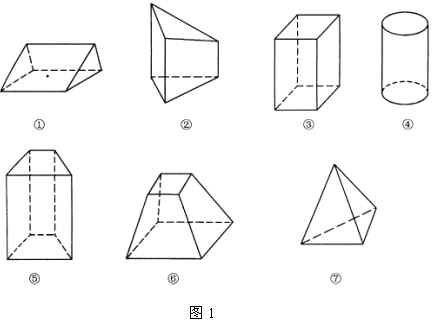
教师指出①③⑤为棱柱,然后问,棱柱有什么样的特征?应当怎么定义呢?
[探索研究]
1.棱柱的概念
(1)概念(出示模型或投影仪)
通过举实际生活中的例子,介绍概念:棱柱的定义、底面、侧面、棱、侧棱、顶点、对角线、高.
(2)棱柱的分类(见图2)
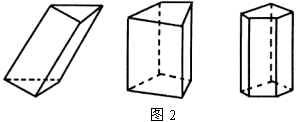
从侧棱与底面的关系来分可分为:斜棱柱、直棱柱、正棱柱.
从底面多边形的边数来分可分为:三棱柱、四棱柱、五棱柱等.
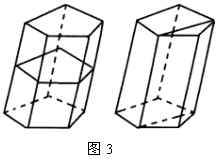
2.棱柱的性质(见图3)
(1)侧棱都相等,侧面是平行四边形.
(2)两个底面与平行于底面的截面是全等的多边形.
(3)过不相邻的两条侧棱的截面是平行四边形.
3.例题分析
例1 下列命题中正确的是( )
A.有两个面平行,其余各面都是四边形的几何体叫棱柱
B.有两个面平行,其余各面都是平行四边形的几何体叫棱柱
C.有两个侧面是矩形的棱柱是直棱柱
D.有两个相邻侧面垂直于底面的棱柱是直棱柱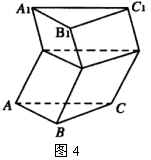
解:如图4,面![]() 面
面![]() ,但图中的几何体中每相邻两个四边形的公共边并不都互相平行,故不是棱柱.
,但图中的几何体中每相邻两个四边形的公共边并不都互相平行,故不是棱柱.![]() 、
、![]() 都不正确.当两个相邻侧面都垂直于底面时,它们的公共侧棱垂直于底面,因此这样的棱柱是直棱柱,故选D.
都不正确.当两个相邻侧面都垂直于底面时,它们的公共侧棱垂直于底面,因此这样的棱柱是直棱柱,故选D.
例2 下列命题中的假命题是( )
A.直棱柱的侧棱就是直棱柱的高
B.有一个侧面是矩形的棱柱是直棱柱
C.直棱柱的侧面是矩形
D.有一条侧棱垂直于底面的棱柱是直棱往
解:A.直棱往的侧棱垂直于底面,是直棱柱的高,命题为真.
B.有一个侧面是矩形,并不能保证侧棱垂直于底面,命题为假.
C.直棱柱的侧面是矩形,命题为真.
D.因棱柱的侧棱相互平行,因此,有一条侧棱垂直于底面,则所有侧棱都垂直于底面,构成直棱柱,命题为真.
故选B.
例3 棱柱成为直棱柱的一个充要条件是( )
A.棱柱有一条侧棱与底面的两边垂直
B.棱柱有一个侧面与底面的一条边垂直
C.棱柱有一个侧面是矩形,且它与底面垂直
D.棱柱的侧面与底面都是矩形
解:A.棱柱有一条侧棱与底面的两边垂直推不出棱柱是直棱柱.(棱柱的一条侧棱与底面的两边垂直,没有明确这两条边是否相交,保证不了测棱与底面垂直.)
B.棱柱有一个侧面与底面的一条边垂直推不出棱柱是直棱柱.(棱柱有一个侧面与底面的一条边垂直,即底面上一条直线与侧面垂直,侧面与底面垂直,保证不了侧棱与底面垂直.)
C.棱柱有一个侧面是矩形,且它与底面垂直.(侧面与底面垂直,侧面又是矩形,根据两平面垂直的性质定理,侧棱垂直于底面.)
D.棱柱是直棱柱推不出棱柱的侧面与底面都是矩形.(棱柱是直棱柱,底面不一定是矩形.)
故选C.
[演练反馈]
1.一个棱柱是正四棱柱的条件是( )
A.底面是正方形,有两个侧面垂直于底面
B.每个侧面是全等的矩形
C.底面是菱形,且有一个顶点处的三条棱两两垂直
D.底面是正方形,有两个侧面是矩形
2.棱柱的侧面是__________形,直棱柱的侧面是__________形,正棱柱的侧面是________形.
3.如图5,直四棱柱![]() 中,各棱长均为
中,各棱长均为![]() ,
,![]() ,求对角线
,求对角线![]() 与
与![]() 的长.
的长.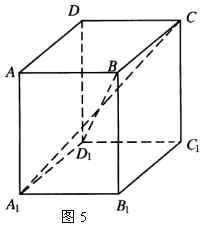
[参考答案]
1.C 2.平行四边形;矩;全等的矩
3.![]() ,
,![]()
[总结提炼]
[学生讨论,教师补充完善.]
1.什么叫棱柱?
2.棱柱的分类.
3.棱柱的性质.
(四)布置作业
1.课本P45习题 9.7 1.
2.课本P45习题 9.7 2.
3.课本P46习题 9.7 3.
[参考答案]
1.略. 2.![]() ,
,![]() 3.
3.![]() ,
,![]()
(五)板书设计
|
1.棱柱的概念(图) 2.棱柱的性质 |
例1 例2 |
例3 |
教学设计示例二
9.7 棱柱 第二课时
教学目标:
1.理解平行六面体、直平行六面体、长方体、正方体的概念.
2.掌握长方体的对角线长与棱长的关系公式.
3.能利用棱柱的概念及性质理解题意,解决问题.
教学过程:
[设置情境]
我们知道长方形的对角线长的平方等于长和宽的平方和,那么长方体的对角线长与其长、宽、高之间有类似的关系吗?
[探索研究]
1.特殊的四棱柱
平行六面体—底面是平行四边形的四棱柱.(如图1(1))
直平行六面体—侧棱与底面垂直的平行六面体.(如图1(2))
长方体—底面是矩形的直平行六面体.(如图1(3))
正方体—棱长都相等的长方体.(如图1(4))
由以上定义不难得到下面的关系:
{正方体} ![]() {长方体}
{长方体}
![]() {直平行六面体}
{直平行六面体} ![]() {平行六面体}
{平行六面体}
2.给出公式
![]() ,其中
,其中![]() 是棱柱的底面积,
是棱柱的底面积,![]() 是棱柱的高.
是棱柱的高.
3.定理
定理 长方体对角线长的平方等于一个顶点上三条棱的长的平方和.
已知:长方体![]() 中,
中,![]() 是一条对角线(如图2)
是一条对角线(如图2)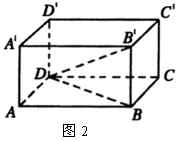
求证:![]() .
.
证明:连结![]() .∵
.∵![]() ,∴
,∴![]() ,
,
又∵![]() ,∴
,∴![]() .
.
4.例题分析
例1 若长方体的三个面的面积分别为![]() 、
、![]() 和
和![]() ,求长方体的对角线长
,求长方体的对角线长![]() .
.
解:设长方体的长、宽、高分别为![]() 、
、![]() 、
、![]() ,对角线长为
,对角线长为![]() ,则
,则
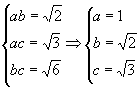
∴![]() .
.
例2 如图1,在正方体![]() 中,
中,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点.
的中点.
(1)求证:![]() ;
;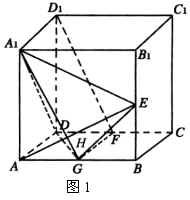
(2)求![]() 与
与![]() 所成的角;
所成的角;
(3)证明:平面![]() 平面
平面![]() .
.
解:(1)由![]() 是正方体,知
是正方体,知![]() 平面
平面![]() .又
.又![]() 平面
平面![]() ,故
,故![]() .
.
(2)取![]() 中点
中点![]() ,连结
,连结![]() 、
、![]() 、
、![]() .由
.由![]() 是
是![]() 中点,知
中点,知![]() ,又
,又![]() ,得
,得![]() ,故
,故![]() 是平行四边形,所以
是平行四边形,所以![]() .
.
设![]() 、
、![]() 交于
交于![]() ,则
,则![]() 是
是![]() 与
与![]() 所成的角.由
所成的角.由![]() 是
是![]() 中点,可得
中点,可得
![]() △
△![]() ≌
≌![]() △
△![]() .
.
∴![]() .故
.故![]() ,即
,即![]() 与
与![]() 所成的角为直角.
所成的角为直角.
(3)![]() ,
,![]() ,又
,又![]() ,故
,故![]() 平面
平面![]() .
.
又![]() 平面
平面 ![]() ,故平面
,故平面![]() 平面
平面![]() .
.
例3 平行六面体![]() 的棱长都相等,且
的棱长都相等,且![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() ,求
,求![]() 到平面
到平面![]() 的距离.
的距离.
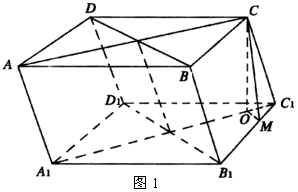 解:(如图1)作
解:(如图1)作![]() 平面
平面![]() 于
于![]() .由
.由![]() 可知
可知![]() 在
在![]() 的角平分线上,又因为
的角平分线上,又因为![]() 是菱形,所以
是菱形,所以![]() 在
在![]() 上,且根据三垂线定理,由
上,且根据三垂线定理,由![]() 得
得![]() ,所以
,所以![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() .
.
(2)作![]() 于
于![]() ,连
,连![]() ,由三垂线定理得
,由三垂线定理得![]() ,在
,在![]() △
△![]() 中,
中,![]() ,
,![]() ,有
,有![]() .
.![]() △
△![]() 中,
中,![]() ,有
,有![]() .于是
.于是![]() .
.
即得![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
[演练反馈]
1.四条对角线不相等且交于一点的四棱柱是( )
A.直四棱柱 B.斜平行六面体 C.长方体 D.正四棱体
2.正方体的对角线长为![]() ,则它的面的对角线长为_____________.
,则它的面的对角线长为_____________.
3.已知正四棱柱![]() 的底面边长为2,侧棱长为
的底面边长为2,侧棱长为![]() .
.
(1)求二面角![]() 的大小;
的大小;
(2)求点![]() 到平面
到平面![]() 的距离.
的距离.
[参考答案]
1.B 2.![]() 3.(1)
3.(1)![]() (2)
(2)![]()
[总结提炼]
掌握特殊四棱柱的概念,弄清它们之间的包含关系,理解长方体的对角线长与棱长的关系,记住柱体的体积公式.
(四)布置作业
1.课本P46习题9.7 4. 2.课本P46习题9.7 5.
3.课本P46习题9.7 7. 4.课本P46习题9.7 8.
[参考答案]
1.提示:(1)利用平行四边形的对角线互相平分来证明.(2)利用(1)的结论.
2.对角线长为![]() . 3.
. 3.![]() .
.
4.略.
(五)板书设计
| 1.特殊的四棱柱(投影图形) 2.定理 |
例1 例2 |
例3 总结 |
教学设计示例三
9.7 棱柱 第三课时
教学目标:
1.掌握水平放置的平面图形的直观图画法.
2.掌握直棱柱的直观图画法.
教具准备:三角板.
教学过程:
[设置情境]
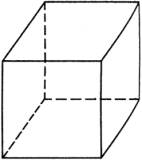 把平面图形画在纸上或黑板上,那很简单.要把立体图形画在纸上或黑板上,实际上是把本来不完全在同一个平面内的点的集合,用同一个平面内的点来表示.这时画在纸上或黑板上的图形,已经不是普通地平面图形,而是立体图形的直观图.
把平面图形画在纸上或黑板上,那很简单.要把立体图形画在纸上或黑板上,实际上是把本来不完全在同一个平面内的点的集合,用同一个平面内的点来表示.这时画在纸上或黑板上的图形,已经不是普通地平面图形,而是立体图形的直观图.
教师问:
(1)右图看起来像什么?
(2)正方体的各个面都是正方形,在此图形中各个面都画成正方形了吗?
(3)立体图形的直观图要有立体感,即把不在同一平面内的点集在同一平面内表现出来,为此,它往往与立体图形的真实形状不相同,那么怎么画立体图形的直观图呢?
[探索研究]
1.水平放置的平面图形的直观图的斜二侧画法
(1)在已知图形中取互相垂直的![]() 轴和
轴和![]() 轴,两轴交于点
轴,两轴交于点![]() .画直观图时,把它们画成对应的
.画直观图时,把它们画成对应的![]() 轴和
轴和![]() 轴,两轴交于点
轴,两轴交于点![]() ,使
,使![]() (或
(或![]() )它们确定的平面表示水平平面.
)它们确定的平面表示水平平面.
(2)已知图形中平行于![]() 轴或
轴或![]() 轴的线段,在直观图中分别画成平行于
轴的线段,在直观图中分别画成平行于![]() 轴或
轴或![]() 轴的线段.
轴的线段.
(3)已知图形中平行于![]() 轴的线段,在直观图中保持原长度不变;平行于
轴的线段,在直观图中保持原长度不变;平行于![]() 轴的线段,长度为原来的一半.
轴的线段,长度为原来的一半.
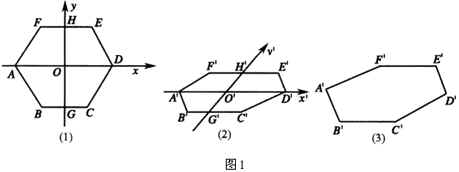
例1 画水平放置的正六边形的直观图.(图1(1))
作法:(1)在已知正六边形![]() 中,取对角线
中,取对角线![]() 所在的直线为
所在的直线为![]() 轴,取对称轴
轴,取对称轴![]() 为
为![]() 轴,两轴交于点
轴,两轴交于点![]() ,画对应的
,画对应的![]() 轴、
轴、![]() 轴,取
轴,取![]() .
.
(2)以点![]() 为中点,在
为中点,在![]() 轴上取
轴上取![]() ,在
,在![]() 轴上取
轴上取![]() ,以点
,以点![]() 为中点画
为中点画![]() 平行于
平行于![]() 轴,且
轴,且![]() ;再以
;再以![]() 为中点画
为中点画![]() 平行于
平行于![]() 轴,且
轴,且![]() .
.
(3)连结![]() 、
、![]() 、
、![]() 、
、![]() ,所得的六边形
,所得的六边形![]() 就是正六边形
就是正六边形![]() 的直观图.(见图1(3))
的直观图.(见图1(3))
2.画直棱柱的直观图
例2 画正六棱柱的直观图.
(画法:见课本第45页.)
[演练反馈]
1.画水平放置的正角形的直观图.
2.画正五棱柱的直观图.
[参考答案]
1.如图2:
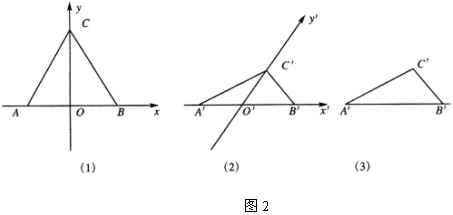
作法:(1)在已知正三角形![]() 中,取
中,取![]() 所在的直线为
所在的直线为![]() 轴,取线段
轴,取线段![]() 的中垂线
的中垂线![]() 所在的直线为
所在的直线为![]() 轴.画对应的
轴.画对应的![]() 轴,
轴,![]() 轴,使
轴,使![]() .
.
(2)以![]() 为中点,在
为中点,在![]() 轴上取
轴上取![]() ,在
,在![]() 轴上
轴上![]() .
.
(3)连结![]() 、
、![]() ,然后擦去辅助线.(见图2(3))
,然后擦去辅助线.(见图2(3))
2.如图3:
作法:1.画轴.画![]() 、
、![]() 、
、![]() 轴,使
轴,使![]() (或
(或![]() ),
),![]() .
.
2.画底面.按![]() 轴、
轴、![]() 轴画正五边形的直观图
轴画正五边形的直观图![]() .
.
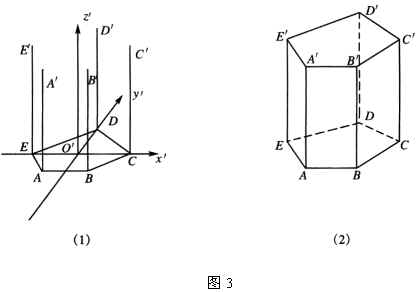
3.画侧棱.过点![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 各点分别作
各点分别作![]() 轴的平行线,并在这些平行线上分别截取
轴的平行线,并在这些平行线上分别截取![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 都等于侧棱长.
都等于侧棱长.
4.成图.顺次连结![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,加以整理,去掉辅助线改被遮挡部分为虚线.(见图3(2))
,加以整理,去掉辅助线改被遮挡部分为虚线.(见图3(2))
[总结提炼]
画水平放置的平面图形的直观图是本节内容的重点.在原平面图形中取![]() 坐标系要本着简便的原则,但这种简便是相对的.事实上,无论
坐标系要本着简便的原则,但这种简便是相对的.事实上,无论![]() 坐标系怎么取(其实可任意取)都能画出与它对应的
坐标系怎么取(其实可任意取)都能画出与它对应的![]() 坐标系,并能找到原坐标系下图形的各顶点在新坐标系
坐标系,并能找到原坐标系下图形的各顶点在新坐标系![]() 下的对应点的位置.
下的对应点的位置.
(四)布置作业
(1)课本P45练习 1.
(2)课本P45练习 2.
(3)课本P46练习 9.7 6.
[参考答案]
略.
(五)板书设计
|
1.平面图形的直观图 (投影) |
例1 2直棱柱的直观图 |
例2 |
教学设计示例四
9.7 棱柱 第四课时
教学目标:
巩固复习棱柱的有关概念和性质.
教学过程:
[复习回顾]
1.棱柱的有关概念.(底面、顶点、棱、高、侧棱、对角面等)
2.特殊的四棱柱的有关概念.
3.长方体的对角线和棱长的关系,柱体的体积公式.
[探索研究]
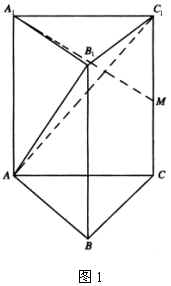
例1 如图1,直棱柱![]() 中,
中,![]()
![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点.求证:
的中点.求证:![]() .
.
证明:∵![]()
又![]() 为直棱柱
为直棱柱
∴![]() 面
面![]()
∴![]()
∴![]() 面
面![]()
欲证![]() ,根据三垂线定理,只须证
,根据三垂线定理,只须证![]()
设![]() ,
,![]() ,
,![]() ,
,![]() ,因
,因![]() ,所以
,所以![]() .于是
.于是![]() ,即得
,即得![]() .
.
例2 若斜三棱柱![]() 的底面是边长为
的底面是边长为![]() 的正三角形,侧棱长为1,
的正三角形,侧棱长为1,![]() .求:
.求:
(1)斜三棱柱![]() 的侧面积;
的侧面积;
(2)侧棱![]() 到平面
到平面![]() 的距离.
的距离.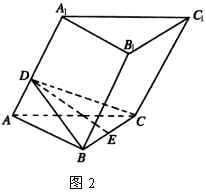
解:(1)如图2,过点![]() 作
作![]() ,交
,交![]() 于
于![]() ,连
,连![]() .因
.因![]() ,
,![]() ,
,![]() 为公共边,∴△
为公共边,∴△![]() ≌△
≌△![]() ,故有
,故有![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() ,
,![]() .又∵
.又∵![]() .所以
.所以![]() 平面
平面![]() ,
,![]() ,故
,故
![]()
![]()
![]()
因为![]() ,
,![]() ,
,![]() ,所以,有
,所以,有
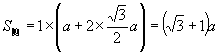 .
.
(2)过![]() 作
作![]() ,
,![]() 交
交![]() 于
于![]() ,则
,则![]() 为
为![]() 中点.因
中点.因![]() ,由(1)知
,由(1)知![]() ,故
,故![]() 平面
平面![]() ,即
,即![]() 为
为![]() 到平面
到平面![]() 的距离.
的距离.
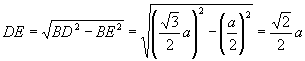 .
.
老师点评:△![]() 实际上就是斜三棱柱
实际上就是斜三棱柱![]() 的直截面.
的直截面.
例3 如图1,正三棱柱![]() 的底面边长为
的底面边长为![]() ,在侧棱
,在侧棱![]() 上截取
上截取![]() ,在侧棱
,在侧棱![]() 上截取
上截取![]() ,过
,过![]() 作截面.
作截面.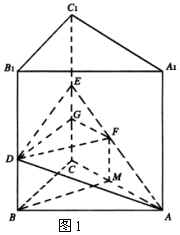
(1)求截面面积;
(2)求证:截面![]() 侧面
侧面![]() .
.
解:(1)因为侧面是矩形所以易求得![]() ,
,![]() ,取
,取![]() 的中点
的中点![]() ,连结
,连结![]() ,则
,则![]() .
.
∴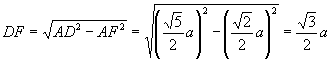
所以![]() .
.
(2)证法一:取![]() 的中点
的中点![]() ,连结
,连结![]() ,则
,则![]() 且
且![]() ,又
,又![]() ,
,![]() ,所以四边形
,所以四边形![]() 是平行四边形,得
是平行四边形,得![]() .
.
∵![]() ,∴
,∴![]() (∵
(∵![]() ),又
),又![]() ,∴
,∴![]() 面
面![]() .
.
∴![]() 面
面![]() ,而
,而![]() 面
面![]()
∴截面![]() 侧面
侧面![]() .
.
证法二:取![]() 中点
中点![]() ,连结
,连结![]() 、
、![]() 易证面
易证面![]() 面
面![]() ,而
,而![]() 面
面![]()
∴![]() ,又
,又![]()
∴![]() 面
面![]()
∴面![]() 侧面
侧面![]()
证法三:(计算二面角![]() 的平面角为
的平面角为![]() )
)
连结![]() ,∵
,∵![]() ,
,![]() 为
为![]() 中点,所以
中点,所以![]() ,所以
,所以![]() 是二面角
是二面角![]() 的平面角,易求得
的平面角,易求得![]() ,
,![]() ,∵
,∵![]() ,∴
,∴![]()
∴面![]() 面
面![]() .
.
教师点评:以棱柱为载体考查线、面之间的位置关系的问题是常见的一种题型.解决这类问题时,必须应用棱柱的有关性质,特别是直棱柱中蕴含着的线、面间的平行和垂直关系.
[演练反馈]
底面是菱形的直菱柱,它的对角线的长分别为9和15,高为5,则棱柱的侧面积为________.
[参考答案]
160.
[总结提炼]
棱柱的定义及性质为我们提供了丰富的已知条件,在解题时要注意灵活运用.
(四)布置作业
1.课本P46习题9.7 9.
2.课本P46习题9.7 10.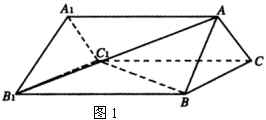
3.如图1,在正三棱柱![]() 中,
中,![]() .
.
(1)求证:![]() ;
;
(2)求二面角![]() 的平面角的正切值.
的平面角的正切值.
4.已知:平行六面体![]() 的底面
的底面![]() 是菱形,且
是菱形,且![]() .
.
(1)证明:![]() ;
;
(2)设![]() ,
,![]() .记面
.记面![]() 为
为![]() ,面
,面![]() 为
为![]() ,求二面角
,求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
[参考答案]
1.![]()
2.![]()
3.略.
4.(1)略. (2)![]()
(五)板书设计
|
1.复习 2.例题 例1 |
例2 例3 |
练习 |