 设为首页
设为首页
 加入收藏
加入收藏
教学设计示例
椭圆及其标准方程(第一课时)
(一)教学目标
掌握椭圆、椭圆的焦点、椭圆的焦距的定义,会推导椭圆的标准方程,能灵活应用椭圆标准形式确定椭圆的标准方程.
(二)教学过程
【情境设置】
前面,我们学习了曲线与方程等知识,哪一位同学回答:
问题1:什么叫做曲线的方程?求曲线的方程一般有哪几个步骤?
对于上述问题的回答.不正确的教师要给予纠正.这样便于学生温故知新,在已有知识的基础上去探求新的知识。
问题2:圆的几何特征是什么?你能否对类似的一些轨迹命题作深入的探索?
一般学生都能回答:“平面内到一个定点的距离为常数的点的轨迹是圆.”对于同学们提出的轨迹命题教师要加以肯定,以鼓励同学们的探索精神.
【探索研究】
1.椭圆的定义
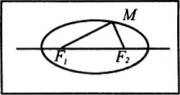 若同学提到了“到两点距离之和等于常数的点的轨迹”。可因势利导进一步问满足这种条件的动点轨迹是什么呢?这时教师示范引导学生绘图.
若同学提到了“到两点距离之和等于常数的点的轨迹”。可因势利导进一步问满足这种条件的动点轨迹是什么呢?这时教师示范引导学生绘图.
取一条一定长的钢绳,把它的两端固定在画板上的
![]() 和
和 ![]() 两点(如图),当绳长大于
两点(如图),当绳长大于 ![]() 和
和 ![]() 间的距离时,用铅笔尖把细绳拉紧,使笔尖在图板慢移动,就可以画出一个椭圆.
间的距离时,用铅笔尖把细绳拉紧,使笔尖在图板慢移动,就可以画出一个椭圆.
通过画图过程,揭示椭圆上的点所要满足的条件.在此基础上,引导学生概括椭圆的定义:
平面内与两个定点 ![]() 、
、 ![]() 的距离的和等于常数(大于
的距离的和等于常数(大于 ![]() )的点轨迹叫做椭圆.这两个定点叫做椭圆的焦点,两焦点的距离叫做椭圆的焦距.
)的点轨迹叫做椭圆.这两个定点叫做椭圆的焦点,两焦点的距离叫做椭圆的焦距.
学生开始只强调椭圆的几何特征—到两个定点
![]() 、
、 ![]() 的距离的和等于常数.这时教师在演示中再从两方面加以强调:
的距离的和等于常数.这时教师在演示中再从两方面加以强调:
①将穿有铅笔的细绳拉到图板平面外,得到的不是椭圆,而是椭球形.使学生认识到必须限制:“在平面内”;
②这里的常数为什么要大于
![]() ?教师边演示边提示学生注意:若常数
?教师边演示边提示学生注意:若常数 ![]() ,则点
,则点 ![]() 的轨迹是线段
的轨迹是线段 ![]()
![]() ,若常数
,若常数 ![]() ,则轨迹不存在.所以要使轨迹是椭圆,必须加上限制条件:“此常数大于
,则轨迹不存在.所以要使轨迹是椭圆,必须加上限制条件:“此常数大于
![]() ”.
”.
2.椭圆的标准方程
1.椭圆的标准方程的推导.
由椭圆的定义,可以知道它的基本几何特征,但对椭圆还具有哪些性质则一无所知.为此需要用坐标法先建立椭圆的方程.
①建系设点
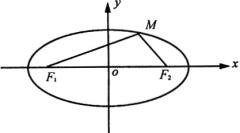 建立坐标系是求曲线方程重要而关键的一步,一般应遵循简单、优化的原则,使点的坐标、几何量的表达式简单化,注意充分利用图形的对称性,使学生认识到以下的选取方法是恰当的.
建立坐标系是求曲线方程重要而关键的一步,一般应遵循简单、优化的原则,使点的坐标、几何量的表达式简单化,注意充分利用图形的对称性,使学生认识到以下的选取方法是恰当的.
以两定点 ![]() 、
、 ![]() 所在直线为
所在直线为 ![]() 轴,线段
轴,线段 ![]()
![]() 的垂直平分线为
的垂直平分线为 ![]() 轴,建立直角坐标系(如图).设
轴,建立直角坐标系(如图).设 ![]() .
. ![]() ,
, ![]() 为椭圆上的任意一点,则
为椭圆上的任意一点,则 ![]() 、
、 ![]() .又设
.又设 ![]() 与
与 ![]() 、
、 ![]() 的距离的和等于
的距离的和等于 ![]() .
.
②点的集合
由定义不难得到椭圆的集合为![]() .
.
③代数方程
![]() .
.
④化简方程
化简方程可请一位反应比较快、书写较规范的同学板演,其余同学在下面完成.教师巡视,适当给予提示:
ⅰ原方程要移项平方,使之抵消部分项,否则相当复杂;一次平方后还含有根式可整理后再平方,化为
![]() ;
;
ⅱ为了使方程简单对称和谐,引入
![]() ,使
,使 ![]() ,从而得到方程
,从而得到方程 ![]() .
.
关于证明所得的方程是椭圆方程,因教材不要求,可从略.
因此,方程 ![]() 即为所求椭圆的标准方程,它表示椭圆的焦点在
即为所求椭圆的标准方程,它表示椭圆的焦点在 ![]() 轴上,焦点是
轴上,焦点是 ![]() 、
、 ![]() .这里
.这里 ![]() .
.
如果使点 ![]() 、
、 ![]() 在
在 ![]() 轴上,点
轴上,点 ![]() 、
、 ![]() 的坐标分别为
的坐标分别为 ![]() 、
、 ![]() ,那么所得方程变为
,那么所得方程变为 ![]()
![]() ,这个方程也是椭圆的标准方程.
,这个方程也是椭圆的标准方程.
2.两种标准方程的比较(引导学生归纳).
两种标准方程中都有 ![]() ,
, ![]() ,因此对于方程
,因此对于方程 ![]() ,只要
,只要 ![]() 、
、 ![]() 、
、 ![]() 同号就是椭圆方程;它们的不同点是椭圆的位置不同,焦点坐标也不相同.由于
同号就是椭圆方程;它们的不同点是椭圆的位置不同,焦点坐标也不相同.由于
![]() ,所以可以根据分母的大小来判定椭圆的焦点在哪一个坐标轴上.分母哪个大,焦点就在哪个轴上.
,所以可以根据分母的大小来判定椭圆的焦点在哪一个坐标轴上.分母哪个大,焦点就在哪个轴上.
(3)例题分析
例1 求适合下列条件的椭圆的标准方程.
①两个焦点的坐标分别是 ![]() 、
、 ![]() ,椭圆上一点到两焦点距离的和等于10.
,椭圆上一点到两焦点距离的和等于10.
②两个焦点的坐标分别是 ![]() 、
、 ![]() ,并且经过点
,并且经过点 ![]() .
.
解:①因为椭圆的焦点在 ![]() 轴上,所以设它的标准方程为
轴上,所以设它的标准方程为 ![]()
![]() .
.
![]() ,
, ![]() ∴
∴
![]() ,
, ![]() ∴
∴
![]()
所以所求椭圆的标准方程为
![]() .
.
②因为椭圆的焦点在 ![]() 轴上,所以设它的标准方程为
轴上,所以设它的标准方程为 ![]()
![]() .
.
由椭圆的定义知: 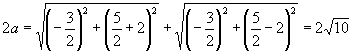
∴ ![]() ,又
,又 ![]() ∴
∴ ![]()
所以所求椭圆的标准方程为
![]() .
.
另法:设所求的标准方程为
![]()
![]()
依题意得 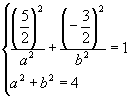
解得 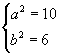
所以所求椭圆的标准方程 ![]() .
.
点评:由已知条件,所求椭圆的标准方程的解题模式是:先确定焦点的位置,设出标准方程(若不能确定焦点的位置,则应分类讨论),再用待定系数法确定
![]() 、
、 ![]() 的值.
的值.
例2 已知 ![]() 、
、 ![]() 是两个定点,
是两个定点, ![]() ,且
,且 ![]() 的周长等于16,求顶点
的周长等于16,求顶点 ![]() 的轨迹方程.
的轨迹方程.
分析:由 ![]() 的周长等于16,
的周长等于16, ![]() 可知,点
可知,点 ![]() 到
到 ![]() 、
、 ![]() 两点的距离的和是常数.因此,点
两点的距离的和是常数.因此,点 ![]() 的轨迹是以
的轨迹是以 ![]() 、
、 ![]() 为焦点的椭圆,可适当建立坐标系求出方程.
为焦点的椭圆,可适当建立坐标系求出方程.
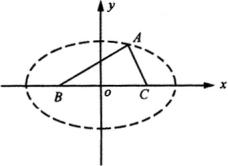 解:如图,建立坐标系,使
解:如图,建立坐标系,使 ![]() 轴经过点
轴经过点 ![]() 、
、 ![]() ,原点
,原点 ![]() 与
与 ![]() 的中点重合.
的中点重合.
由已知
![]() .
.
![]() ,有
,有
![]() .
.
即点 ![]() 的轨迹是椭圆,且
的轨迹是椭圆,且 ![]() ,
, ![]() .
.
∴ ![]() ,
, ![]() ,
, ![]() .
.
但当点 ![]() 在直线
在直线 ![]() 上,即
上,即 ![]() 时,
时, ![]() 、
、 ![]() 、
、 ![]() 三点不能构成三角形,所以点
三点不能构成三角形,所以点 ![]() 的轨迹方程是
的轨迹方程是![]()
![]() .
.
点评:①求出曲线的方程后,要注意检查一下方程的曲线上的点是否都符合题意,如果不符合题意的点,应在所得方程后注明限制条件.
②变题1°.已知 ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 成等差数列,求点
成等差数列,求点 ![]() 的轨迹方程.
的轨迹方程.
2°,在 ![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,求顶点
,求顶点 ![]() 的轨迹方程.
的轨迹方程.
第1°题 ![]() 、
、 ![]() 、
、 ![]() 三点不必构成三角形,就不应限制
三点不必构成三角形,就不应限制 ![]() ,2°,
,2°, ![]() (
( ![]() ,
, ![]() ,
, ![]() 为
为 ![]() 的三边)应注意能构成三角形.
的三边)应注意能构成三角形.
(三)随堂练习
1.平面内两个定点的距离等于8,一个动点
![]() 到这两个定点的距离的和等于10,建立适当的坐标系,写出动点
到这两个定点的距离的和等于10,建立适当的坐标系,写出动点
![]() 的轨迹方程.
的轨迹方程.
2.如果椭圆 ![]() 上一点
上一点 ![]() 到焦点
到焦点 ![]() 的距离等于6,则点
的距离等于6,则点 ![]() 到另一个焦点
到另一个焦点 ![]() 的距离是___________.
的距离是___________.
3.写出适合下列条件的椭圆的标准方程:
① ![]() ,
, ![]() ,焦点在
,焦点在 ![]() 轴上;
轴上;
② ![]() ,
, ![]() ,焦点在
,焦点在 ![]() 轴上;
轴上;
③ ![]() ,
, ![]() .
.
答案:1. ![]() 2.14
2.14
3.① ![]() ②
②
![]() ③
③ ![]() 或
或 ![]() .
.
(四)总结提炼
1.椭圆的定义:平面内与两个定点
![]() 、
、 ![]() 的距离的和等于常数
的距离的和等于常数 ![]() 的点的轨迹是椭圆.
的点的轨迹是椭圆.
当 ![]() 时,动点的轨迹为线段
时,动点的轨迹为线段 ![]() ,当
,当 ![]() 时,动点不存在.
时,动点不存在.
2.椭圆的标准方程
焦点在 ![]() 轴上椭圆的标准方程为
轴上椭圆的标准方程为 ![]()
![]() .
.
焦点在 ![]() 轴上椭圆的标准方程为
轴上椭圆的标准方程为 ![]()
![]() .
.
焦点所在坐标轴由分母大小对应分子的变量来确定.
3. ![]() 、
、 ![]() 、
、 ![]() 之间的关系是
之间的关系是 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 、
、 ![]() 大小不确定.
大小不确定.
(五)布置作业
1.椭圆 ![]() 上一点
上一点 ![]() 到一个焦点的距离等于3,则它到另一个焦点的距离为(
)
到一个焦点的距离等于3,则它到另一个焦点的距离为(
)
A.5 B.7 C.8 D.10
2.椭圆 ![]() 的焦距是2,则
的焦距是2,则 ![]() 的值等于(
)
的值等于(
)
A.5或3 B.5 C.8 D.16
3.焦点坐标为(0,-4)、(0,4),
![]() 的椭圆的标准方程为_________________.
的椭圆的标准方程为_________________.
4.已知椭圆 ![]()
![]() ,
, ![]() 、
、 ![]() 是它的焦点,
是它的焦点, ![]() 是过
是过 ![]() 的直线与椭圆交于
的直线与椭圆交于 ![]() 、
、 ![]() 两点,则
两点,则 ![]() 的周长为__________________.
的周长为__________________.
5.化简下列方程,使结果不含根式:
(1) ![]() .
.
(2) ![]() .
.
6.动点 ![]() 到两个定点
到两个定点 ![]() 、
、 ![]() 的距离的和是
的距离的和是 ![]() ,求动点
,求动点 ![]() 的轨迹方程.
的轨迹方程.
答案:1.B 2.A
3. ![]() 4.
4. ![]()
5.(1) ![]() (2)
(2) ![]() 6.
6.
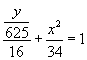
(六)板书设计
|
8.1 椭圆及其标准方程(一) |
||
| 1.椭圆的定义 2.椭圆的标准方程 (1)标准方程的推导 |
(2)标准方程的比较 例1. |
例2. 学生练习 |
教学设计示例
椭圆及其标准方程(第二课时)
(一)教学目标
能根据条件熟练地求出椭圆的标准方程,借助椭圆方程巩固求曲线方程的一般方法,并能根据条件对一些点进行取舍,学会利用中间变量(相关点)求轨迹方程或轨迹.
(二)教学过程
(请两位学生回答,教师板书)
问题1.椭圆的定义是什么?
平面内到两个定点 ![]() 、
、 ![]() 的距离的和等于常数(大于
的距离的和等于常数(大于 ![]() )的点的轨迹.
)的点的轨迹.
问题2.椭圆的标准方程是怎样的?
当焦点在 ![]() 轴上时为
轴上时为 ![]()
![]() ;
;
当焦点在 ![]() 轴上时为
轴上时为 ![]()
![]() .
.
由椭圆的定义和标准方程可知,确定椭圆的标准方程需要三个条件,除需要指明焦点位置外,还要求出 ![]() 、
、 ![]() 的值.
的值.
【探索研究】
例1 求焦点在坐标轴上,且经过
![]() 和
和 ![]() 两点的椭圆的标准方程.
两点的椭圆的标准方程.
分析:由题设条件焦点在哪一个坐标轴上不明确,椭圆的标准方程有两种情形.为了计算简便,可设其方程 ![]()
![]() ,而不必考虑焦点位置,直接可求出方程:
,而不必考虑焦点位置,直接可求出方程:
由一位学生板演完成,解答为:
设所求的椭圆方程为 ![]()
![]() ,
,
由 ![]() 和
和 ![]() 两点在椭圆上可得
两点在椭圆上可得
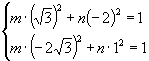 即
即 ![]()
解得 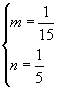
故所求的椭圆方程为 ![]() .
.
点评:不明确焦点在哪一个坐标轴上时,通常应进行分类讨论,但计算较繁,一般可设所求的椭圆方程为 ![]()
![]() ,不必考虑焦点位置,用待定函数法求出
,不必考虑焦点位置,用待定函数法求出 ![]() 、
、 ![]() 的值即可.
的值即可.
例2 ![]() 的两个顶点坐标分别是
的两个顶点坐标分别是 ![]() 和
和 ![]() ,另两边
,另两边 ![]() 、
、 ![]() 的斜率的乘积是
的斜率的乘积是 ![]() ,求顶点
,求顶点 ![]() 的轨迹方程.
的轨迹方程.
解:设顶点 ![]() 的坐标为
的坐标为 ![]()
依题意得 ![]() .
.
∴顶点 ![]() 的轨迹方程为
的轨迹方程为 ![]() .
.
点评(1)不少学生会误认为椭圆的焦点就是 ![]() 、
、 ![]() 与推导出的方程表示焦点在
与推导出的方程表示焦点在 ![]() 轴,椭圆矛盾,因而对正确性产生怀疑.说明这里顶点
轴,椭圆矛盾,因而对正确性产生怀疑.说明这里顶点 ![]() 的轨迹显然是椭圆但不直接满足椭圆的定义.
的轨迹显然是椭圆但不直接满足椭圆的定义.
 (2)此题可以推广为:
(2)此题可以推广为: ![]() 的两顶点坐标分别是
的两顶点坐标分别是 ![]() 和
和 ![]()
![]() ,另两边
,另两边 ![]() 、
、 ![]() 的斜率的乘积是
的斜率的乘积是 ![]() ,求顶点
,求顶点 ![]() 的轨迹方程,请读者自己完成.
的轨迹方程,请读者自己完成.
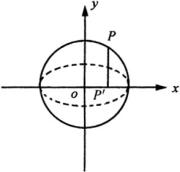
例3 如图,已知一个圆的圆心为坐标原点,半径为2.从这个圆上任意一点
![]() 向
向 ![]() 轴作垂线段
轴作垂线段 ![]() ,求线段
,求线段 ![]() 中点
中点 ![]() 的轨迹.
的轨迹.
解:设点 ![]() 的坐标为
的坐标为 ![]() ,点
,点 ![]() 的坐标为
的坐标为 ![]() ,则
,则 ![]() ,
, ![]() .
.
因为 ![]() 在圆
在圆 ![]() 上,所以
上,所以 ![]() ①
①
将![]() ,
, ![]() 代入方程①得
代入方程①得
![]() 即
即 ![]()
所以点 ![]() 的轨迹是一个椭圆.
的轨迹是一个椭圆.
点评:(1)在求点 ![]() 的轨迹方程时,也可寻找
的轨迹方程时,也可寻找 ![]() 、
、 ![]() 与中间变量
与中间变量 ![]() 、
、 ![]() 之间的关系.利用已知关于
之间的关系.利用已知关于 ![]() 、
、 ![]() 之间关系的方程,得到关于
之间关系的方程,得到关于 ![]() 、
、 ![]() 的方程,这种利用中间变量求点的轨迹方程的方法也是常用的方法.
的方程,这种利用中间变量求点的轨迹方程的方法也是常用的方法.
(2)由本题的结论可以看出,将圆按照某个方向均匀地压缩(拉长),可以得到椭圆.
例4 一动圆与已知圆
![]() 外切,圆
外切,圆 ![]() 内切,试求这动圆圆心的轨迹方程.
内切,试求这动圆圆心的轨迹方程.
分析:两圆相切时,圆心之间的距离与两圆的半径有关,可以找到动圆圆心满足的条件.
由一位学生板演,教师巡视,同时启发学生分析.解答如下:
显然两定圆的圆心和半径分别为
![]() ,
, ![]() ;
; ![]() ,
, ![]() .
.
设动圆圆心为 ![]() ,半径为
,半径为 ![]() ,则由题设有
,则由题设有
![]() .
. ![]() ∴
∴ ![]() .
.
由椭圆定义可知 ![]() 在以
在以 ![]() ,
, ![]() 为焦点的椭圆上.
为焦点的椭圆上.
![]() ,
, ![]() , ∴
, ∴ ![]() .
.
故动圆圆心的轨迹方程为 ![]() .
.
(三)随堂练习
1.以两条坐标轴为对称轴的椭圆过点 ![]() 和
和 ![]() ,则此椭圆方程是( )
,则此椭圆方程是( )
A. ![]() B.
B. ![]()
C. ![]() 或
或 ![]() D.以上都不对
D.以上都不对
2.已知椭圆的方程是 ![]()
![]() ,它的两个焦点分别为
,它的两个焦点分别为 ![]() 、
、 ![]() ,则
,则 ![]() ,弦
,弦 ![]() 过
过 ![]() ,则
,则 ![]() 的周长为( )
的周长为( )
A.10 B.20
C. ![]() D.
D. ![]()
3.已知一定圆 ![]() 及其内一异于圆心
及其内一异于圆心 ![]() 的定点
的定点 ![]() ,过点
,过点 ![]() 且与圆
且与圆 ![]() 相切的动圆圆心
相切的动圆圆心 ![]() 的轨迹是( )
的轨迹是( )
A.直线 B.线段 C.圆 D.椭圆
答案:1.A 2.D 3.D
(四)总结提炼
1.在求椭圆的标准方程时,必须先确定焦点的位置,选择相应的标准方程,然后再根据条件求出 ![]() 、
、 ![]() 的值;若动点的轨迹满足椭圆定义时,可直接用定义写出方程,而不必要去重复繁琐的化简.
的值;若动点的轨迹满足椭圆定义时,可直接用定义写出方程,而不必要去重复繁琐的化简.
2.在求一些椭圆的方程时,要注意一些特殊点的取舍,将圆按照某个方向均匀地压缩(拉长),可以得到椭圆.
(五)布置作业
1.如果方程 ![]() 表示焦点在
表示焦点在 ![]() 轴上的椭圆,那么实数
轴上的椭圆,那么实数 ![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.(0,2)
C.
B.(0,2)
C. ![]() D.(0,1)
D.(0,1)
2.过点(3,-2)且与 ![]() 有相同焦点的椭圆方程是( )
有相同焦点的椭圆方程是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
3.若方程 ![]() 表示焦点在
表示焦点在 ![]() 轴上的椭圆,则
轴上的椭圆,则 ![]() ,
, ![]() 应满足的条件为__________________.
应满足的条件为__________________.
4.点 ![]() 是椭圆
是椭圆 ![]() 上一点,以点
上一点,以点 ![]() 以及焦点
以及焦点 ![]() 、
、 ![]() 为顶点的三角形的面积等于1,则
为顶点的三角形的面积等于1,则 ![]() 点的坐标为_______________.
点的坐标为_______________.
5.从圆 ![]() 上任意一点
上任意一点 ![]() 向
向 ![]() 轴作垂线段
轴作垂线段 ![]() ,且线段
,且线段 ![]() 上一点
上一点 ![]() 满足关系式
满足关系式 ![]()
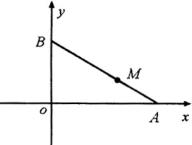 ,求点
,求点 ![]() 的轨迹.
的轨迹.
6.如图,线段 ![]() 的两端
的两端 ![]() 、
、 ![]() 分别在
分别在 ![]() 轴、
轴、 ![]() 轴上滑动,
轴上滑动, ![]() ,点
,点 ![]() 是
是 ![]() 上一点,且
上一点,且 ![]() ,点
,点 ![]() 随线段
随线段 ![]() 的运动而变化,求点
的运动而变化,求点 ![]() 的轨迹方程.
的轨迹方程.
答案:1.D 2.A 3. ![]() .
.
4. 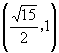 或
或 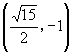 或
或 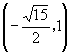 或
或 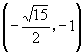 .
.
5. ![]() .
.
6.设 ![]() ,
, ![]() ,
, ![]()
依题意得 ![]() .
.
由 ![]() 得
得 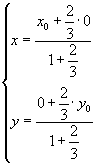 即
即 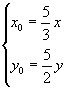
∴ ![]() 即
即 ![]()
这就是 ![]() 点的轨迹方程.
点的轨迹方程.
(六)板书设计
|
8.1 椭圆及其标准方程(二) |
||
|
(一)复习提问 问题1 问题2 (二)椭圆标准方程的求法 |
(三)例题分析 例1. 例2. 例3. |
例4. 练习1 练习2 (四)小结 |