 设为首页
设为首页
 加入收藏
加入收藏
含有绝对值的不等式
教学目标
理解 ![]() 及其两个推论,并能应用它证明简单含有绝对值不等式的证明问题。
及其两个推论,并能应用它证明简单含有绝对值不等式的证明问题。
教学重点难点
重点是理解掌握定理及等号成立的条件,绝对值不等式的证明。
难点是定理的推导过程的探索,摆脱绝对值的符号,通过定理或放缩不等式。
教学过程
一、复习引入
我们在初中学过绝对值的有关概念,请一位同学说说绝对值的定义。
当 ![]() 时,则有:
时,则有: 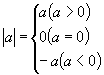
那么 ![]() 与
与 ![]() 及
及 ![]() 的大小关系怎样?
的大小关系怎样?
这需要讨论 当 ![]()
当 ![]()
当 ![]()
综上可知: ![]()
我们已学过积商绝对值的性质,哪位同学回答一下?
![]() .
.
当 ![]() 时,有:
时,有: ![]() 或
或 ![]() .
.
二、引入新课
由上可知,积的绝对值等于绝对值的积;商的绝对值等于绝对值的商。
那么和差的绝对值等于绝对值的和差吗?
1.定理探索
和差的绝对值不一定等于绝对值的和差,我们猜想
![]() .
.
怎么证明你的结论呢?
用分析法,要证 ![]() .
.
只要证 ![]()
即证 ![]()
即证 ![]() ,
,
而 ![]() 显然成立,
显然成立,
故 ![]()
那么怎么证 ![]() ?
?
同样可用分析法
当 ![]() 时,显然成立,
时,显然成立,
当 ![]() 时,要证
时,要证 ![]()
只要证 ![]() ,
,
即证 ![]()
而 ![]() 显然成立。
显然成立。
从而证得 ![]() .
.
还有别的证法吗?(学生讨论,教师提示)
由 ![]() 与
与 ![]() 得
得 ![]() .
.
当我们把 ![]() 看作一个整体时,上式逆用
看作一个整体时,上式逆用 ![]() 可得什么结论?
可得什么结论?
![]() 。
。
能用已学过得的 ![]() 证明
证明 ![]() 吗?
吗?
可以 ![]() 表示为
表示为 ![]()
![]() .
.
即 ![]() (教师有计划地板书学生分析证明的过程)
(教师有计划地板书学生分析证明的过程)
就是含有绝对值不等式的重要定理,即 ![]() .
.
由于定理中对 ![]() 两个实数的绝对值,那么三个实数和的绝对值呢?
两个实数的绝对值,那么三个实数和的绝对值呢? ![]() 个实数和的绝对值呢?
个实数和的绝对值呢?
亦成立 ![]()
![]()
![]()
这就是定理的一个推论,由于定理中对 ![]() 没有特殊要求,如果用
没有特殊要求,如果用 ![]() 代换
代换 ![]() 会有什么结果?(请一名学生到黑板演)
会有什么结果?(请一名学生到黑板演)
![]() ,
,
用 ![]() 代
代 ![]() 得
得 ![]() ,
,
即 ![]() 。
。
这就是定理的推论 ![]() 成立的充要条件是什么?
成立的充要条件是什么?
![]()
那么 ![]() 成立的充要条件是什么?
成立的充要条件是什么?
![]() .
.
例1 已知 ![]() ,求证
,求证 ![]() . (由学生自行完成,请学生板演)
. (由学生自行完成,请学生板演)
证明: ![]()
![]()
![]()
![]()
![]()
例2 已知 ![]() ,求证
,求证 ![]() .
.
证明: ![]()
![]()
点评:这是为今后学习极限证明做准备,要习惯和“配凑”的方法。
例3 求证 ![]() .
.
证法一:(直接利用性质定理)在 ![]() 时,显然成立.
时,显然成立.
当 ![]() 时,左边
时,左边 
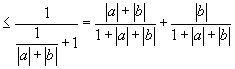
![]() .
.
证法二:(利用函数的单调性)研究函数 ![]() 在
在 ![]() 时的单调性。
时的单调性。
设 ![]() ,
,
![]() ,
, ![]() 在
在 ![]() 时是递增的.
时是递增的.
又 ![]() ,将
,将 ![]() ,
, ![]() 分别作为
分别作为 ![]() 和
和 ![]() ,则有
,则有
![]() (下略)
(下略)
证法三:(分析法)原不等式等价于![]() ,
,
只需证 ![]() ,
,
即证 ![]()
又 ![]() ,
,
![]() 显然成立.
显然成立.
![]() 原不等式获证。
原不等式获证。
还可以用分析法证得 ![]() ,然后利用放缩法证得结果。
,然后利用放缩法证得结果。
三、随堂练习
1.①已知 ![]() ,求证
,求证 ![]() .
.
②已知 ![]() 求证
求证 ![]() .
.
2.已知 ![]() 求证:
求证:
① ![]() ;
;
② ![]() .
.
3.求证 ![]() .
.
答案:1. 2. 略
3. ![]() 与
与 ![]() 同号
同号 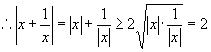
四、小结
1.定理 ![]() . 把
. 把 ![]() 、
、 ![]() 、
、 ![]() 看作是三角形三边,很象三角形两边之和大于第三边,两边之差小于第三边,这样理解便于记忆,此定理在后面学习复数时,可以推广到比较复数的模长,并有其几何意义,有时也称其为“三角形不等式”.
看作是三角形三边,很象三角形两边之和大于第三边,两边之差小于第三边,这样理解便于记忆,此定理在后面学习复数时,可以推广到比较复数的模长,并有其几何意义,有时也称其为“三角形不等式”.
2.平方法能把绝对值不等式转化为不含绝对值符号的不等式,但应注意两边非负时才可平方,有些证明并不容易去掉绝对值符号,需用定理 ![]() 及其推论。
及其推论。
3.对 ![]() 要特别重视.
要特别重视.
五、布置作业
1.若 ![]() ,则不列不等式一定成立的是( )
,则不列不等式一定成立的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
2.设 ![]() 为满足
为满足 ![]() 的实数,那么( )
的实数,那么( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
3.能使不等式 ![]() 成立的正整数
成立的正整数 ![]() 的值是__________.
的值是__________.
4.求证:
(1) ![]() ;
;
(2) ![]() .
.
5.已知 ![]() ,求证
,求证 ![]() .
.
答案:1. D 2. B 3.1、2、3
4. ![]()
![]()
5. 
= ![]()
注:也可用分析法.
六、板书设计
|
6.5含有绝对值的不等式(一) |
||
|
1.复习 2.定理 推论 |
例1 例2 |
例3 课堂训练 |