第六节 互斥事件有一个发生的概率

教学建议

（一）教材分析

1．知识结构

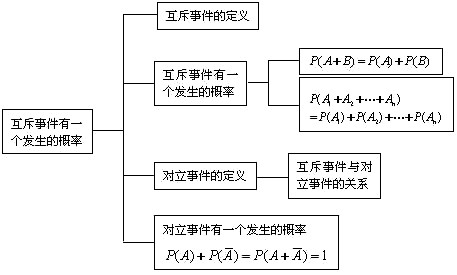
2．重点难点分析

　　重点是互斥事件的概率加法公式的理解及运用的前提条件；难点是用定义判断较复杂的事件是否互斥，突破重点和难点的关键是正确运用集合与分类的思想方法判断较复杂的事件的互斥与对立。

　　（1）互斥事件的概率计算．

　　一般地，如果事件 彼此互斥，那么事件 发生（即 中有一个发生）的概率，等于这 个事件分别发生的概率的和，即

　　当直接计算某一事件的概率较为复杂时，可转而先求其对立事件的概率，可使概率的计算得到简化．

　　（2）对互斥事件、对立事件的理解．

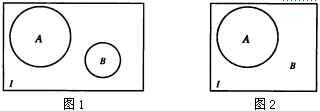
　　从集合角度看，事件 、 互斥，就是它们相应集合的交集是空集（如图1）；事件 、 对立，就是事件 包含的结果的集合是其对立事件 包含的结果的补集（如图2）．

　　（3）互斥事件与对立事件的区别和联系．

　　互斥事件和对立事件都是对两个事件而言的，它们有区别又有联系．在一次试验中，两个互斥的事件有可能都不发生，也可能有一个发生；而两个对立的事件则必有一个发生，但不可能同时发生．所以，两个事件互斥，它们未必对立；反之，两个事件对立，它们一定互斥．也就是说，两个事件对立是这两个事件互斥的充分不必要条件．

　　（4）怎样区分互斥事件与对立事件

　　不能同时发生的事件 与 称为互斥事件。例如某事件 ：某班今天下午第一节是语文课，事件 ：该班今天下午第一节是数学课。这两个事件不可能同时发生，故 、 是互斥事件时，那么 、 同时发生的概率为0，而对立事件是互斥事件的特殊情况，是指两个互斥事件 与 ，必有一个发生的事件．事件 的对立事件记作： ，对立事件是针对两个事件．一般地，两个事件对立是这两事件互斥的充分不必要条件．若 、 是对立事件，则 与 互斥，且A＋ （A、 中至少有一个发生的事件）是必然事件．如事件 ：某班今天下午第一节是数学课与事件 ：某班今天下午第一节不是数学课是对立事件．

　　从集会的角度看，几个事件彼此互斥，是指由各个事件所含的结果组成的集合彼此交集是空集，事件 的对立事件 所包含的结果组成的集合，是全集中由事件 所包含的结果组成的集合的补集．

　　（5）如何正确使用互斥事件的概率加法公式

　　如果事件 、 互斥，则： ．

　　如果事件 是彼此互斥事件，则：

　　特别地，若A、 是对立事件，则： ＝1，即：

　　要想灵活运用此公式，必须把公式的含意理解透彻，如：在某一试验中，共有 种等可能基本事件，其中事件 包含 个基本事件，事件 包含有 个基本事件．当 、 互斥时则 中基本事件和 中基本事件不存在相同的结果，事件 ＋ 的发生表示 与 中有一个发生．这就是说： 中的这 种结果，和 中的这 种结果中，有任意一个发生就表示事件 发生了．所以： 。又因为： ，故 这里是针对等可能事件证明的．但这公式对以后所学的互斥事件均成立，并可推广到几个彼此互斥事件的情形．

　　从集会角度来看，事件 、 互斥，指事件 、 所含结果组成的集合交集为空集，所有事件的结果构成全集U，则：

　　　

　　　　　　　　

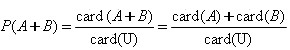
（二）教法建议

　　（1）建议从生活示例引入互斥事件，以引起学生的学习兴趣，并同时指出学习互斥事件的概率的必要性，也让学生体会到数学是来源于生活又应用于生活中；

　　（2）教学时要让学生搞清几个相联系的概念的意义，比如互斥事件、对立事件等，只有弄清事件之间的关系类型，才能做到准确利用公式．

　　（3）教学要注意让学生记准一些符号及其意义，比如“事件 ，表示事件 与事件 中至少有一个发生，而我们往往会想当然地认为是事件 与 同时发生，事实上当 与 互斥时，它们不可能同时发生．

　　（4）要注重典型例题的教学，通过实例教学，让学生加深对概念的理解，逐步掌握一些具体的解题方法．