第三节 函数的图象

教学建议

　　1、教材分析

　　(1)知识结构

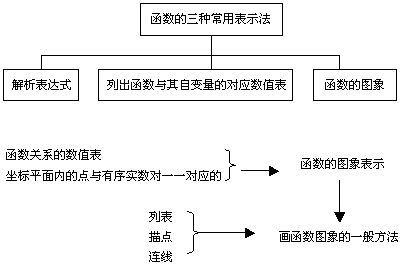
　　(2)重点、难点分析

　　本节内容的重点是：能画出简单函数的图象.由函数关系的数值表与坐标平面内的点与有序实数对间的一一对应关系联想到函数还可以用图象来表示.函数有它的“形”的一面.学习函数图象的画法，其重点并不在于画图本身，而是通过画图，进一步体会函数的意义，为今后的进一步学习打下良好的基础.逐渐达到能够利用函数图象研究函数的性质，解决实际问题.真正领会数形结合的思想，达到“数”与“形”的灵活转化，并有一定的看图说图能力.

　　本节内容的难点也是画出简单函数的图象和渗透数形结合的思想.画函数图象对学生来说比较陌生，接受起来会有一定的困难.尤其是对函数还不太理解的同学，往往会消极对待.有的同学仅能记下画函数图象的一般步骤，老师要求画图时才画.不会主动利用函数图象解题.这样对数形的理解还停留在操作的技能层面上，没有转化成自己的思想.因此，数形结合思想的渗透是一个难点，需要教师的精心设计.

　　2、教法建议

　　现代建构主义的理论认为，新知识的形成首先源于个人对新知识的主观建构，因此，教师必须为学生提供必要的背景知识，并与学生一道探索新的知识.具体说明如下：

　　（1）本节课从一个具体的函数实例，由函数解析式引出函数对应值表，即列表法.其实在现实生活中也有很多类似的例子，如公共汽车的价目表.为方便乘客与售票，制作成梯形表格的形式，一目了然.教师可以根据学生的熟悉的情况，由学生举出例子.并从中体会y与x的对应关系，即y与x满足函数关系.给个x值就有一个相应的y值.

　　（2）学生由于第一次画函数图象，会碰到一些具体问题.如：描出几个点后，究竟该怎样连结这几个点.画多少个点为好等.学生能够提出问题，并产生怀疑说明它已经具备了一些数学能力，的确在实际画图时，不能仅凭列表、描点、连线.还要考虑函数本身的性质.由于学生在知识上的限制，本节只给出一些简单函数的图象.如一次函数的图象是一条直线，在画图的过程中可以让学生逐步体会到它的一些性质.因此，建议教师在讲授这部分内容时，可与学生共同画图或让学生板书.既体会函数的概念，又掌握画函数图象的一般方法.

　　（3）现代信息技术在中小学已经普及，借助计算机我们可以快速地画出许多函数的图象.手工描点画图究竟还有没有意义呢？可以说，它的意义不在描点画图本身，而在于它所蕴涵的数形结合的数学思想方法.数形结合的思想一方面体现在已知函数解析式，画出它的图象来.另一方面也体现在，由函数图象，直观地得出函数的一些性质.看图识图的能力成为我们培养的重点.教师可以从其它学科与现实生活中选取一些例子.既激发了学生学习数学的兴趣，由渗透了数学思想方法.

返回页首