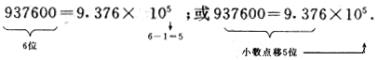第十节 有理数的乘方　

教学建议

　　(一)重点、难点分析

　　本节教学的重点是熟练进行有理数的乘方运算；本节教学的难点是理解有理数乘方运算的符号法则．

　　1．乘方是特殊的乘法运算，其特殊性就是相乘的因数都相同；

　　2．乘方运算的结果叫做幂，幂的性质是：正数的任何次幂是正数；负数的奇次幂是负数，负数的偶次幂是正数；

　　3．有理数的乘方运算与有理数的加减乘除一样，首先要确定幂的符号，然后再计算幂的绝对值；

　　4．一个数的科学记数法中，10的指数比原数的整数位数少1．如原数有8位整数，指数就是7．

　　（二）知识结构

　　

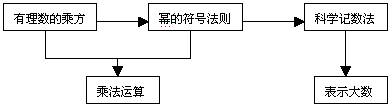
　　（三）教法建议

　　1．正确理解乘方的意义。

　　表示个相乘的积，如：表示3个2相乘，即：。一定记住：。

　　2．注意与二者的区别及相互关系。

　　（1）区别：底数为，表示个相乘的积；底数为，表示个相乘的积的相反数，如：；而。

　　（2）关系：当为偶数时，与互为相反数，当为奇数时，与相等。如：，；，。

　　3．注意与的区别

　　表示个相乘的积，而表示个相乘的积再除以的商。

　　如：，

　　4．掌握科学记数法。

　　把一个大于10的数写成科学记数法的形式，是一个大于或等于1且小于10的数。10的指数是比原数的整数部分少1的数，也可以看作是原数变为时，小数点移动的位数。如：

返回页首