 设为首页
设为首页
 加入收藏
加入收藏
扩展资料
寻找二面角的平面角的方法
二面角是高中立体几何中的一个重要内容,也是一个难点.对于二面角方面的问题,学生往往无从下手,他们并不是不会构造三角形或解三角形,而是没有掌握寻找二面角的平面角的方法.
我们试将寻找二面角的平面角的方法归纳为以下六种类型.
一、根据平面角的定义找出二面角的平面角
例1 在 ![]() 的二面角
的二面角
![]() 的两个面内,分别有
的两个面内,分别有 ![]() 和
和 ![]() 两点.已知
两点.已知 ![]() 和
和 ![]() 到棱的距离分别为2和4,且线段
到棱的距离分别为2和4,且线段 ![]() ,试求:
,试求:
(1)直线 ![]() 与棱
与棱 ![]() 所构成的角的正弦值;
所构成的角的正弦值;
(2)直线 ![]() 与平面
与平面 ![]() 所构成的角的正弦值.
所构成的角的正弦值.
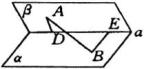
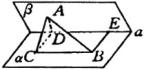
分析:求解这道题,首先得找出二面角的平面角,也就是找出
![]() 角在哪儿.如果解决了这个问题,这道题也就解决了一半.
角在哪儿.如果解决了这个问题,这道题也就解决了一半.
根据题意,在平面 ![]() 内作
内作 ![]() ;在平面
;在平面 ![]() 内作
内作 ![]() ,
, ![]() ,连结
,连结 ![]() 、
、 ![]() .可以证明
.可以证明 ![]() ,则由二面角的平面角的定义,可知
,则由二面角的平面角的定义,可知 ![]() 为二面角
为二面角 ![]() 的平面角.以下求解略.
的平面角.以下求解略.
二、根据三垂线定理找出二面角的平面角
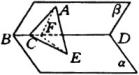 例2
如图,在平面
例2
如图,在平面 ![]() 内有一条直线
内有一条直线 ![]() 与平面
与平面 ![]() 成
成 ![]() ,
, ![]() 与棱
与棱 ![]() 成
成 ![]() ,求平面
,求平面 ![]() 与平面
与平面 ![]() 的二面角的大小.
的二面角的大小.
分析:找二面角的平面角,可过 ![]() 作
作 ![]() ;
; ![]() 平面
平面 ![]() ,连结
,连结 ![]() .由三垂线定理可证
.由三垂线定理可证 ![]() ,则
,则 ![]() 为二面角的平面角.
为二面角的平面角.
总结:(1)如果两个平面相交,有过一个平面内的一点与另一个平面垂直的垂线,可过这一点向棱作垂线,连结两个垂足.应用三垂线定理可证明两个垂足的连线与棱垂直,那么就可以找到二面角的平面角.
(2)在应用三垂线定理寻找二面角的平面角时,注意“作”、“连”、“证”,即“作
![]() ”、“连结
”、“连结 ![]() ”、“证明
”、“证明 ![]() ”.
”.
三、作二面角棱的垂面,垂面与二面角的两个面的两条交线所构成的角,即为二面角的平面角
例3 如图1,已知 ![]() 为
为 ![]() 内的一点,
内的一点, ![]() 于
于 ![]() 点,
点, ![]() 于
于 ![]() 点,如果
点,如果 ![]() ,试求二面角
,试求二面角 ![]() 的平面角.
的平面角.
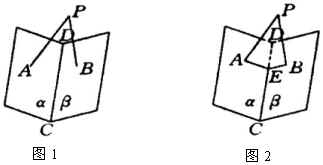
分析: ![]() 平面
平面 ![]() .
.
因此只要把平面 ![]() 与平面
与平面 ![]() 、
、 ![]() 的交线画出来即可.证明
的交线画出来即可.证明 ![]() 为
为 ![]() 的平面角,
的平面角, ![]() (如图2).
(如图2).
注意:这种类型的题,如果过 ![]() 作
作 ![]() ,垂足为
,垂足为 ![]() ,连结
,连结 ![]() ,我们还必须证明
,我们还必须证明 ![]() ,及
,及 ![]() 为平面图形,这样做起来比较麻烦.
为平面图形,这样做起来比较麻烦.
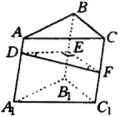 例4
已知斜三棱柱
例4
已知斜三棱柱 ![]() 中,平面
中,平面 ![]() 与平面
与平面 ![]() 构成的二面角的平面角为
构成的二面角的平面角为 ![]() ,平面
,平面 ![]() 与平面
与平面 ![]() 构成的二面角为
构成的二面角为 ![]() .试求平面
.试求平面 ![]() 与平面
与平面 ![]() 构成的二面角的大小.
构成的二面角的大小.
分析:作三棱柱的直截面,可得△ ![]() ,其三个内角分别为斜三棱柱的三个侧面两两构成的二面角的平面角.
,其三个内角分别为斜三棱柱的三个侧面两两构成的二面角的平面角.
总结:对棱柱而言,其直截面与各个侧棱的交点所形成的多边形的各个内角,分别为棱柱相邻侧面构成的二面角的平面角.
四、平移平面法
例5 如图,正方体 ![]() 中,
中, ![]() 为
为 ![]() 的中点,
的中点, ![]() 为
为 ![]() 上的点,且
上的点,且 ![]() .设正方体的棱长为
.设正方体的棱长为 ![]() ,求平面
,求平面 ![]() 与底面
与底面 ![]() 构成的锐角的正切.
构成的锐角的正切.
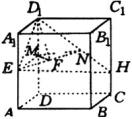 分析:本题中,仅仅知道二面角棱上的一点
分析:本题中,仅仅知道二面角棱上的一点
![]() ,在这种情况下,寻找二面角的平面角较困难.根据平面平移不改变它与另一个平面构成的角的大小的原理,如果能把二面角中的一个平面平移,找出辅助平面与另一个平面的交线,就可以作出二面角的平面角.有了平面角之后,只需要进行常规构造三角形和解三角形的计算,就可以解决问题了.
,在这种情况下,寻找二面角的平面角较困难.根据平面平移不改变它与另一个平面构成的角的大小的原理,如果能把二面角中的一个平面平移,找出辅助平面与另一个平面的交线,就可以作出二面角的平面角.有了平面角之后,只需要进行常规构造三角形和解三角形的计算,就可以解决问题了.
如图,过点 ![]() 作
作 ![]() 与
与 ![]() 相交于
相交于 ![]() 点,过
点,过 ![]() 点作
点作 ![]() ,与
,与 ![]() 相交于
相交于 ![]() 点.可证平面
点.可证平面 ![]() 平面
平面 ![]() .这样,求平面
.这样,求平面 ![]() 与平面
与平面 ![]() 的二面角的平面角就转化为求平面
的二面角的平面角就转化为求平面 ![]() 与平面
与平面 ![]() 的二面角的平面角.显然
的二面角的平面角.显然 ![]() 为这两个平面的交线,过点
为这两个平面的交线,过点 ![]() 作
作 ![]() ,
, ![]() 为垂足,连结
为垂足,连结 ![]() ,可证
,可证 ![]() .则
.则 ![]() 为本题要寻找的二面角.
为本题要寻找的二面角.
五、找垂面,作垂线
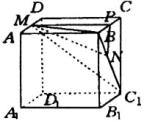 例6
如图,正方体
例6
如图,正方体 ![]() 中,
中, ![]() 为棱
为棱 ![]() 的中点,求平面
的中点,求平面 ![]() 和平面
和平面 ![]() 所构成的锐二面角的正切.
所构成的锐二面角的正切.
分析:平面 ![]() 与二面角
与二面角 ![]() 的一个面
的一个面 ![]() 垂直,与另一个平面
垂直,与另一个平面 ![]() 相交,过
相交,过 ![]() 点作
点作 ![]() ,垂足为
,垂足为 ![]() ,过
,过 ![]() 作
作 ![]() ,交
,交 ![]() 于
于 ![]() 点,连结
点,连结 ![]() ,由三垂线定理可证
,由三垂线定理可证 ![]() ,则
,则 ![]() 为二面角
为二面角 ![]() 的平面角.
的平面角.
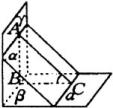 总结:当一个平面与二面角的一个平面垂直,与另一个平面相交时,往往过这个面上的一点作这两个垂直平面交线的垂线,再过垂足作二面角棱的垂线.根据三垂线定理即可证明,并找出二面角的平面角.
总结:当一个平面与二面角的一个平面垂直,与另一个平面相交时,往往过这个面上的一点作这两个垂直平面交线的垂线,再过垂足作二面角棱的垂线.根据三垂线定理即可证明,并找出二面角的平面角.
再如图,要找 ![]() 所构成的二面角的平面角,可找平面
所构成的二面角的平面角,可找平面 ![]() ,且
,且 ![]() ,
, ![]() ,过
,过 ![]() 上任何一点
上任何一点 ![]() 作
作 ![]() ,垂足为
,垂足为 ![]() ,过
,过 ![]() 作
作 ![]() ,垂足为
,垂足为 ![]() ,连结
,连结 ![]() ,可证
,可证 ![]() 为
为 ![]() 的平面角.
的平面角.
六、根据特殊图形的性质找二面角的平面角
1.三线合一
 例7
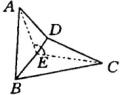
如图,空间四边形
例7
如图,空间四边形 ![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .试求
.试求 ![]() 二面角的余弦值.
二面角的余弦值.
分析:如图, ![]() ,
, ![]() ,则△
,则△ ![]() 和△
和△ ![]() 为等腰三角形.过
为等腰三角形.过 ![]() 作
作 ![]() ,垂足为
,垂足为 ![]() ,连结
,连结 ![]() .根据三线合一,且
.根据三线合一,且 ![]() 为
为 ![]() 中点,可证
中点,可证 ![]() ,则
,则 ![]() 为二面角
为二面角 ![]() 的平面角.
的平面角.
2.全等
 例8
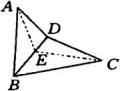
如图,已知空间四边形
例8
如图,已知空间四边形 ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .试求
.试求 ![]() 的余弦值.
的余弦值.
分析:过 ![]() 作
作 ![]() ,垂足为
,垂足为 ![]() ,连结
,连结 ![]() .根据已知条件,△
.根据已知条件,△ ![]() 和△
和△ ![]() 全等,可证
全等,可证 ![]() ,则
,则 ![]() 为二面角
为二面角 ![]() 的平面角.
的平面角.
3.二面角的棱蜕化成一点
例9 如图,四棱锥 ![]() 中,
中, ![]() 和
和 ![]() 与面
与面 ![]() 垂直,△
垂直,△ ![]() 为正三角形.
为正三角形.
(1)若 ![]() 时,求面
时,求面 ![]() 与面
与面 ![]() 的夹角;
的夹角;
(2)若 ![]() 时,求面
时,求面 ![]() 与面
与面 ![]() 的夹角.
的夹角.
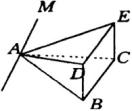 分析:如图,面
分析:如图,面 ![]() 与面
与面 ![]() 的交线蜕化成一点,但面
的交线蜕化成一点,但面 ![]() 与面
与面 ![]() 与面
与面 ![]() 相交.如果三个平面两两相交,它们可能有三种情况:(1)交线为一点;(2)一条交线;(3)三条交线互相平行.在图1中,两条交线
相交.如果三个平面两两相交,它们可能有三种情况:(1)交线为一点;(2)一条交线;(3)三条交线互相平行.在图1中,两条交线
![]() 与
与 ![]() 互相平行,所以肯定有过
互相平行,所以肯定有过 ![]() 且平行于
且平行于 ![]() 的一条交线.
的一条交线.
可过 ![]() 作
作 ![]() ,平面
,平面
![]() 与平面
与平面 ![]() 的交线即为
的交线即为 ![]() .过
.过 ![]() 作
作 ![]() 于
于 ![]() ,过
,过 ![]() 作
作 ![]() 于
于 ![]() .可证
.可证 ![]() ,
, ![]() ,则
,则 ![]() 为面
为面 ![]() 与面
与面 ![]() 的夹角.
的夹角.
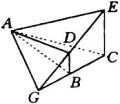 如图,
如图, ![]() 与
与 ![]() 不平行且相交.根据三个平面两两相交可能出现的三种情况,这三个面的交线为一点.延长
不平行且相交.根据三个平面两两相交可能出现的三种情况,这三个面的交线为一点.延长
![]() 、
、 ![]() 相交于
相交于 ![]() 点,连结
点,连结 ![]() .
. ![]() 即为平面
即为平面 ![]() 与平面
与平面 ![]() 的交线,通过一些关系可证
的交线,通过一些关系可证 ![]() 为平面
为平面 ![]() 与平面
与平面 ![]() 的夹角.
的夹角.
通过以上分析和举例说明,寻找二面角的平面角的方法就比较容易了.只要我们勤动脑,善观察,多总结,抓住问题的特征,找出适当的方法,关于二面角的平面角的问题就会迎刃而解.
解决二面角问题的“金氏平面”法
众所周知,解决二面角问题,寻找或求作二面角的平面角是关键.平面角如何作,作在什么位置上,往往是困难所在.传统的做法较多地从线的角度理解平面角,有时难免一叶障目,不见森林.本文拟从面面关系的角度认识平面角,把二面角的平面角看成面面相交的结果,试图由此产生一种先见森林,后见树木的效果.
为了行文方便,故且将与二面角的两个面都垂直的平面,称作金氏平面;将与二面角的一个面垂直而与二面角的另一个面相交的平面,称作银氏平面.关于金氏平面有如下结果:
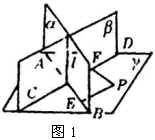
定理1 二面角的棱垂直于金氏平面.
已知:平面![]() 与平面
与平面![]() 的交线为
的交线为![]() ,平面
,平面![]() 与
与![]() 、
、![]() 都垂直,求证:
都垂直,求证:![]() .
.
证明 如图1,设![]() ,
,![]() .在平面
.在平面![]() 上取一点
上取一点![]() ,且点
,且点![]() 不在直线
不在直线![]() 上,也不在直线
上,也不在直线![]() 上,过点
上,过点![]() 作
作![]() 于
于![]() ,作
,作![]() 于
于![]() .
.
由![]() ,
,![]() 知,
知,![]() ,∴
,∴![]() ;同理,
;同理,![]() .∴
.∴![]() .
.
由定理1可知,金氏平面与二面角两个面的交线构成的角就是二面角的平面角,于是得到寻找二面角的平面角的第一种方法:在图中找一个与二面角的两个面都垂直的平面,则此平面与二面角两个面的交线构成的角就是二面角的平面角.
例1 如图2,在正三棱柱![]() 中,
中,![]() 点在
点在![]() 上,截面
上,截面![]() 侧面
侧面![]() .若
.若![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成二面角(锐角)的度数.(1996年高考题)
所成二面角(锐角)的度数.(1996年高考题)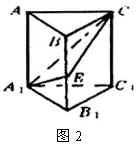
分析 此题用金氏平面法极易看出![]() 就是所求二面角的平面角.要是单纯地从线线关系的角度去看,即便是这样现成的平面角也往往会视而难见,甚至视而不见.
就是所求二面角的平面角.要是单纯地从线线关系的角度去看,即便是这样现成的平面角也往往会视而难见,甚至视而不见.
解 显然,侧面![]() 底面
底面![]() ,又已知侧面
,又已知侧面![]() 截面
截面![]() ,侧面
,侧面![]() 是所求二面角的金氏平面,因而其与二面角两个面的交线构成的角
是所求二面角的金氏平面,因而其与二面角两个面的交线构成的角![]() 就是所求二面角的平面角.由等腰
就是所求二面角的平面角.由等腰![]() △
△![]() 可得
可得![]() .
.
定理2 垂直于二面角之棱的平面是金氏平面.
证明略.
由定理2可得寻找二面角的平面角的第二种方法:在图中找一个与二面角的棱垂直的平面,则此平面与二面角的两个面的交线构成的角就是该二面角的平面角.
有些二面角问题,图中虽然没有现成的金氏平面,却有现成的银氏平面,在这种情况下,可以利用银氏平面构作出金氏平面.
例2 设直二面角![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,求二面角
,求二面角![]() 的大小(如图3).
的大小(如图3).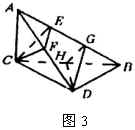
分析 有意识地寻找银氏平面对解决本问题至关重要,容易看出图中有两个银氏平面:面![]() 和面
和面![]() ,据此可以给出两种解法.
,据此可以给出两种解法.
解法1 由面![]() 面
面![]() ,
,![]() 知,
知,![]() 面
面![]() ,
,![]() .又
.又![]() ,∴
,∴![]() 面
面![]() ,故面
,故面![]() 面
面![]() ,面
,面![]() 是银氏平面.
是银氏平面.
在面![]() 上,过
上,过![]() 作
作![]() 于
于![]() ,过
,过![]() 作
作![]() 的垂面交
的垂面交![]() 于
于![]() ,则面
,则面![]() 就是金氏平面,
就是金氏平面,![]() 是二面角的平面角.
是二面角的平面角.
设![]() ,在
,在![]() △
△![]() 中,可得
中,可得![]() ,在
,在![]() △
△![]() 中可得
中可得![]() ,在
,在![]() △
△![]() 中,
中,![]() .在
.在![]() △
△![]() 中,
中,![]() ,因此所求二面角的平面角是
,因此所求二面角的平面角是![]() .
.
解法2 面![]() 面
面![]() ,
,![]() 知,
知,![]() 面
面![]() .又
.又![]() ,∴
,∴![]() .
.
设![]() ,在
,在![]() △
△![]() 中,可得
中,可得![]() ,
,![]() .在
.在![]() △
△![]() 中,可得
中,可得![]() ,在
,在![]() △
△![]() 中,可得
中,可得![]() ,在
,在![]() △
△![]() 中,
中,![]() ,因此所求二面角的大小为
,因此所求二面角的大小为![]() .
.
例3 如图4,已知直角三角形![]() 的两直角边
的两直角边![]() ,
,![]() ,
,![]() 为斜边
为斜边![]() 上一点.沿
上一点.沿![]() 将此直角三角形折成直二面角
将此直角三角形折成直二面角![]() .此时
.此时![]() ,求二面角
,求二面角![]() 的大小.
的大小.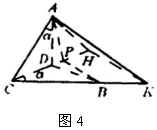
解 过棱![]() 上一点
上一点![]() 作棱
作棱![]() 的垂面,交
的垂面,交![]() 的延长线于
的延长线于![]() ,交
,交![]() 的延长线于
的延长线于![]() ,则
,则![]() 就是二面角的平面角.
就是二面角的平面角.
由![]() 面
面![]() 知,
知,![]() ,
,![]() .在面
.在面![]() 上作
上作![]() ,由面
,由面![]() 面
面![]() 知,
知,![]() 面
面![]() ,
,![]() .故
.故![]() 面
面![]() ,
,![]() ,
,![]() .
.
设![]() ,则
,则![]() .
.
在![]() △
△![]() 中,
中,![]() ,
,![]() .
.
在△![]() 中,
中,![]()
![]()
在![]() △
△![]() 中,由
中,由![]() ,可得
,可得![]() .
.
在![]() △
△![]() 中,
中,![]() ,
,
∴![]() .
.
在![]() △
△![]() 中,由余弦定理可得
中,由余弦定理可得![]() .
.
在![]() △
△![]() 中,
中,![]() .
.
在![]() △
△![]() 中,
中,![]() ,故所求二面角的大小是
,故所求二面角的大小是![]() .
.
顺便指出,由例3的解答过程可知,![]() ,
,![]() ,所以例3的平面角也可以这样构作:在平面
,所以例3的平面角也可以这样构作:在平面![]() 上作
上作![]() 交
交![]() 的延长线于
的延长线于![]() ,在平面
,在平面![]() 上作
上作![]() 交
交![]() 的延长线于
的延长线于![]() ,连结
,连结![]() ,则
,则![]() 就是二面角的平面角.此作法如果没有金氏平面作铺垫就稍显突兀,不易想到,但有金氏平面的铺垫就成为自然之事了.
就是二面角的平面角.此作法如果没有金氏平面作铺垫就稍显突兀,不易想到,但有金氏平面的铺垫就成为自然之事了.
总之,金氏平面法用来确定二面角的平面角的位置是比较直观简便的.但由于现行教材并无金氏平面之说,因此在实际解题时金氏平面法所确定的平面角宜作策略性的利用:(1)当金氏平面所确定的平面角在图中已经存在时,则此平面角就是我们证明的目标,如例1;(2)当金氏平面所确定的平面角在图中尚没有时,则可据此平面角设计出适当的方法构作平面角.