 设为首页
设为首页
 加入收藏
加入收藏
扩展资料
抛物线的切线与割弦的关系
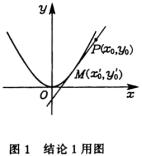
结论1 设 ![]() ,过抛物线
,过抛物线 ![]() 外一点
外一点 ![]() 作抛物线的切线,设
作抛物线的切线,设 ![]() 是切点则有以下关系:
是切点则有以下关系:
![]()
其中 ![]() 是
是 ![]() 点处的切线斜率,在数值上有
点处的切线斜率,在数值上有 ![]()
 证 设切点为
证 设切点为 ![]() ,设切线方程为
,设切线方程为 ![]() ,由
,由 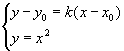 消去
消去 ![]() 得
得
![]()
![]()
![]()
![]()
![]() 在切线上,
在切线上,
![]()
![]()
![]()
又以 ![]() 为切点的切线的斜率为
为切点的切线的斜率为 ![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
推论1 如果抛物线方程为
![]() ,则有以下关系式
,则有以下关系式
![]() ,
, ![]() (
( ![]() 是切线的斜率),
是切线的斜率), 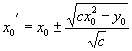 。
。
推论2 如果抛物线方程为 ![]() ,同样可以证得以下关系式
,同样可以证得以下关系式
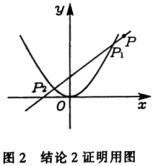
![]()
证 ![]() 在直线上,
在直线上, ![]() ,现求
,现求 ![]() 的交点,得
的交点,得 ![]()
![]() 上式说明
上式说明 ![]() 与
与 ![]() 的横坐标一定是在
的横坐标一定是在 ![]() 的左右,而且距离相等为
的左右,而且距离相等为 ![]() 。
。
观察:
![]()
![]()
![]()
![]()
![]()
同理可得
![]()
![]()
![]()
![]()
而 ![]()
![]()
![]()
![]()
![]()
![]()
由(1),(2)式可知:
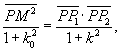
即
![]()
(其中 ![]() 为切线斜率,等于
为切线斜率,等于 ![]() ,
, ![]() 为割线斜率)
为割线斜率)
该公式形如图的切割线定理,乘以 ![]() 为参变数的系数。
为参变数的系数。
结论3 设过 ![]() 作抛物线
作抛物线 ![]() 的两条割线为
的两条割线为 ![]() ,分别交抛物线于
,分别交抛物线于 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 。则由(3)可得
。则由(3)可得
![]()
即 ![]() (其中
(其中 ![]() ,
, ![]() 为两割线的斜率)。
为两割线的斜率)。
对于一般的二次曲线都可用上述方法,利用平移,旋转得到相关的结论。
扩展资料
奇妙的弹道曲线
弹道曲线是炮弹飞行的轨迹,它是一种极常见而又极重要的曲线.
一个射出物的轨迹,依赖于发射时的初速度 ![]() 与发射时的仰角
与发射时的仰角 ![]() .取发射点为原点,射向的水平方向为
.取发射点为原点,射向的水平方向为 ![]() 轴的正方向,建立直角坐标系.设
轴的正方向,建立直角坐标系.设 ![]() 秒钟后,炮弹发射后的位置在点
秒钟后,炮弹发射后的位置在点 ![]() ,由匀速直线运动与竖直上抛运动可知,弹道曲线的参数方程是
,由匀速直线运动与竖直上抛运动可知,弹道曲线的参数方程是
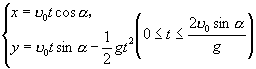 . (1)
. (1)
其中 ![]() 是炮弹从发射起到落地止所用的时间.由(1)消去参数
是炮弹从发射起到落地止所用的时间.由(1)消去参数 ![]() ,就得到弹道轨迹的普通方程:
,就得到弹道轨迹的普通方程:
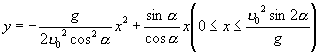 . (2)
. (2)
它是一段抛物线.在(1),(2)中,若 ![]() 取不同的值,就得到不同的抛物线.它们称它为抛物线族.
取不同的值,就得到不同的抛物线.它们称它为抛物线族.
弹道曲线族有下面一些奇妙的性质.
1.同时圆
在(1)中,把 ![]() 看成参数,消去
看成参数,消去 ![]() 可得
可得
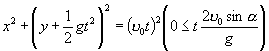 . (3)
. (3)
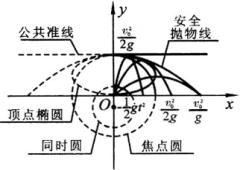 它表明,在同一平面内,以相同的发射速度从同一地点发射的许多抛物体,尽管发射的角度大小不同,但经过相等的时间后,这些物体到达同一圆周上,如图.这个圆以
它表明,在同一平面内,以相同的发射速度从同一地点发射的许多抛物体,尽管发射的角度大小不同,但经过相等的时间后,这些物体到达同一圆周上,如图.这个圆以 ![]() 为圆心,以
为圆心,以 ![]() 为半径,而此半径恰好等于在相同时间
为半径,而此半径恰好等于在相同时间 ![]() 内平抛运动中的水平距离.这是弹道曲线族的运动学特征之一.
内平抛运动中的水平距离.这是弹道曲线族的运动学特征之一.
2.顶点椭圆
将(2)式配方得
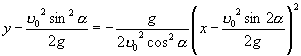 , (4)
, (4)
可得出抛物线族顶点所在的曲线的参数方程
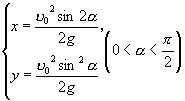 . (5)
. (5)
消去参数 ![]() ,得
,得
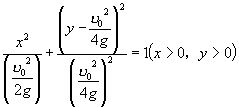 (6)
(6)
它可以看成是椭圆 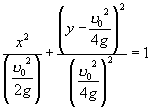 按向量
按向量 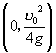 平移得到.它表明,虽然抛物线族的顶点位置随着发射角
平移得到.它表明,虽然抛物线族的顶点位置随着发射角 ![]() 的大小不同而改变,但所有顶点都在一个固定的半椭圆上.这个椭圆的中心在
的大小不同而改变,但所有顶点都在一个固定的半椭圆上.这个椭圆的中心在 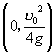 ,长轴平长于
,长轴平长于 ![]() 轴,长轴长是短轴长的2倍,而短轴长恰好等于物体竖直上抛所能达到的最大高度,这就是抛物线族顶点的运动学意义.我们称这个椭圆为“顶点椭圆”.据(5)可知,当
轴,长轴长是短轴长的2倍,而短轴长恰好等于物体竖直上抛所能达到的最大高度,这就是抛物线族顶点的运动学意义.我们称这个椭圆为“顶点椭圆”.据(5)可知,当 ![]() 时,顶点组成半椭圆的下半弧;当
时,顶点组成半椭圆的下半弧;当 ![]() 时,顶点组成半椭圆的上半弧.如上图.
时,顶点组成半椭圆的上半弧.如上图.
3.焦点圆
抛物线(4)可看成是抛物线
![]() , (7)
, (7)
按向量 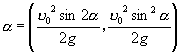 平移得到.
平移得到.
易求出抛物线(7)的焦点坐标为 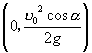 ,准线方程为
,准线方程为 ![]() ,将它们也按
,将它们也按 ![]() 平移,就得抛物线(4)的焦点坐标为
平移,就得抛物线(4)的焦点坐标为 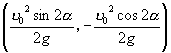 ,准线方程为
,准线方程为 ![]() .
.
故抛物线族(4)的焦点所在曲线的轨迹方程为
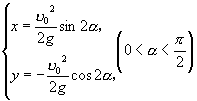 . (8)
. (8)
消去 ![]() ,得
,得
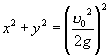 . (9)
. (9)
它表明,虽然抛物线族的焦点位置随着发射角 ![]() 的大小不同而改变,但所有焦点都在一个固定的半圆上,这个圆以原点为圆心,以
的大小不同而改变,但所有焦点都在一个固定的半圆上,这个圆以原点为圆心,以 ![]() 为半径,而此半径恰好等于物体竖直上抛时所能达到的最大高度。这就是抛物线族焦点的运动学意义,我们称这个圆为“焦点圆”.由(8)可知,当
为半径,而此半径恰好等于物体竖直上抛时所能达到的最大高度。这就是抛物线族焦点的运动学意义,我们称这个圆为“焦点圆”.由(8)可知,当 ![]() 时,焦点组成半圆的下半弧;当
时,焦点组成半圆的下半弧;当 ![]() 时,焦点组成半圆上半弧.见上图.
时,焦点组成半圆上半弧.见上图.
4.公共准线
由前可知,抛物线族(4)的准线方程为
![]() .
.
它表明,准线方程与发射角无关,即不论发射角大小如何。抛物线族的准线总是一条固定的直线,而此直线恰好是将物体竖直上抛时所能达到的最高点处的一条水平线,这就是抛物线族准线的运动学意义.我们称这条直线为“公共准线”.公共准线与顶点椭圆与焦点圆均相切.
5.安全线
把(2)整理成关于 ![]() 的二次方程
的二次方程
![]() . (10)
. (10)
这个方程如果有实数解,就表示抛物线族(2)中有抛物线存在.该方程的判别式为
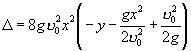 ,
,
显然有:
![]() 方程(10)有两个相同实数解;
方程(10)有两个相同实数解;
![]() 方程(10)无实数解;
方程(10)无实数解;
![]() 方程(10)有两个不同实数解;
方程(10)有两个不同实数解;
它表明,除原点外,当且仅当点 ![]() 分别在抛物线
分别在抛物线
![]() (11)
(11)
的上方、上面、下方时,抛物线族(1)中,就分别设有抛物线、有且只有一条抛物线、有两条抛物线通过该点.
矿山爆破中,为了确保安全,需要确定危险区和安全区.爆破点处炸开的矿石可看成以相等的初速度沿各种射角 ![]() (这里
(这里 ![]() )被抛射出去,矿石运动的轨道,就是抛物线族(1).上面证明了这些抛物线不会越出一定的范围.范围以外为安全区,这个范围的边界就是抛物线(11),我们把它称为“安全抛物线”,如公园内喷泉最外面的轮廓线.
)被抛射出去,矿石运动的轨道,就是抛物线族(1).上面证明了这些抛物线不会越出一定的范围.范围以外为安全区,这个范围的边界就是抛物线(11),我们把它称为“安全抛物线”,如公园内喷泉最外面的轮廓线.
扩展资料
从离心率看圆锥曲线间的关系
早在17世纪初,在当时关于一个数学对象能从一个形状连续地变到另一个形状的新思想的影响下,法国天文学家开普勒对圆锥曲线的性质作了新的阐述.他发现了圆锥曲线的焦点和离心率,并指明抛物线还有一个在无穷远处的焦点,直线是圆心在无穷远处的圆.从而他第一个掌握了这样的事实:椭圆、抛物线、双曲线、圆,都可以从其中的一个连续地变为另一个,从而辩证地看到了各类圆锥曲线间的关系.
下面我们从离心率对圆锥曲线的形状的影响入手,来研究圆锥曲线间的关系,为了讨论这个问题,我们首先在同一直角坐标系中把椭圆、抛物线、双曲线这三种曲线的方程统一起来.
1.椭圆、抛物线、双曲线的统一方程
将椭圆 ![]() 按向量
按向量 ![]() 平移得到
平移得到
![]() ,
,
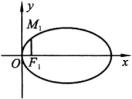 即
即
![]() .
.
作椭圆的半通径(即过椭圆焦点且垂直于长轴的半弦) ![]() ,用
,用 ![]() 表示
表示 ![]() ,易证
,易证 ![]() ,同时易知
,同时易知 ![]() .
.
故椭圆的方程可写成
![]() .
.
类似地,将双曲线 ![]() 按向量
按向量 ![]() 平移得到
平移得到
![]() ,
,
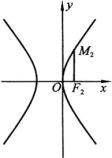 即
即
![]() .
.
作双曲线的半通径(即过双曲线焦点且垂直于实轴的半弦) ![]() ,用
,用 ![]() 表示
表示 ![]() ,易证
,易证 ![]() ,同时易知
,同时易知 ![]() .
.
故双曲线方程可写成
![]() .
.
对于抛物线 ![]() ,
, ![]() 为半通径长,离心率
为半通径长,离心率 ![]() ,它也可写成
,它也可写成
![]() ,
,
于是在同一坐标系下,三种曲线有统一方程
![]() ,
,
 其中
其中 ![]() 是曲线的半通径长,当
是曲线的半通径长,当 ![]() ,
, ![]() ,
, ![]() 时分别表示椭圆、抛物线、双曲线.
时分别表示椭圆、抛物线、双曲线.
2.从离心率看圆锥曲线间的关系
设椭圆、双曲线、抛物线有相同的半通径,即统一方程中的 ![]() 不变,令离心率
不变,令离心率 ![]() 变化,在这种情况下,我们讨论曲线变化趋势.
变化,在这种情况下,我们讨论曲线变化趋势.
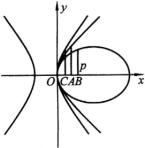
在同一坐标系下,作出这三种曲线如图所示,设 ![]() ,
, ![]() ,
, ![]() 分别是抛物线焦点、椭圆的左焦点和双曲线的右焦点,则有
分别是抛物线焦点、椭圆的左焦点和双曲线的右焦点,则有
![]() ,
,
![]() ,
,
![]() ,
,
所以 ![]() .
.
这说明 ![]() 点在
点在 ![]() 点右侧,而
点右侧,而 ![]() 点在
点在 ![]() 点左侧.
点左侧.
由此,我们来看三种曲线的位置关系(由曲线的对称性,只考虑第一象限内的情况),从统一方程不难看出,当任意取定 ![]() 时,设椭圆、抛物线和双曲线上对应点的纵坐标分别为
时,设椭圆、抛物线和双曲线上对应点的纵坐标分别为 ![]() ,
, ![]() ,
, ![]() ,有
,有
![]() .
.
这说明,双曲线在抛物线上侧,而椭圆在抛物线下侧.
下面我们进一步讨论圆锥曲线间的关系.
(1)当离心率 ![]() 由小于1无限趋近于1时,
由小于1无限趋近于1时,
![]() .(符号“→”表示无限趋近于).
.(符号“→”表示无限趋近于).
即 ![]() .
.
这说明椭圆的左焦点无限趋近于抛物线的焦点,且椭圆在第一象限内向上移动无限接近抛物线.
又因为 ![]() ,所以
,所以
![]() .
.
由于 ![]() 由小于1无限趋近于1,所以
由小于1无限趋近于1,所以 ![]() .
.
这说明椭圆右焦点沿 ![]() 轴正向趋于无限远.因此可以看出,在椭圆的情况下,当
轴正向趋于无限远.因此可以看出,在椭圆的情况下,当 ![]() 时,椭圆的极限情况就是抛物线.
时,椭圆的极限情况就是抛物线.
(2)当离心率 ![]() 由大于1无限趋近于1时,
由大于1无限趋近于1时,
![]() ,
,
即 ![]() .
.
这说明双曲线右焦点无限接近于抛物线的焦点,且双曲线右支在第一象限内向下移动无限接近抛物线.
又因为 ![]() ,所以
,所以
![]() .
.
由于 ![]() 由大于1无限趋近于1,所以
由大于1无限趋近于1,所以 ![]() .
.
这说明双曲线左焦点沿 ![]() 轴负方向趋于无限远.因此可以看出,在双曲线的情况下,当
轴负方向趋于无限远.因此可以看出,在双曲线的情况下,当 ![]() 时,双曲线的极限情况就是抛物线.
时,双曲线的极限情况就是抛物线.
(3)在椭圆情况下,当 ![]() 时有
时有
![]() ,
,
![]() ,
, ![]() ,
, ![]() .
.
故当 ![]() 时,椭圆的极限情况是以点
时,椭圆的极限情况是以点 ![]() 为圆心、以
为圆心、以 ![]() 为半径的圆.这个事实也可以从统一方程中,令
为半径的圆.这个事实也可以从统一方程中,令 ![]() ,得到的就是这个圆的方程:
,得到的就是这个圆的方程:
![]() .
.