第二节 直线的方程

一      次    式

　　直线的方程

　　是一次方程．它的左边 是 、 的一次式．为方便起见，常数 也看作是一次式．

　　显然，如果 的一次式 在 与 时取相同的值，那么 必定是常数 （即 必定为零）．这一个简单的事实有许多应用．

　　例1  求证等腰三角形底边上一点到两边距离之和为定值．

　　解  设底边 为 轴，腰 、 的法线式为

　　及

　　并且 的内部在这两条直线的正侧．点 在线段 上，它的坐标为（ ，0）．因此， 到两腰的距离之和为

                  （10.1）

　　是 的一次式．

　　由于当 与 或 重合时，（10.1）的值均为腰上的高 ，所以（10.1）式是常数 ．

　　注意点到直线的距离是有正负的．当 沿 轴移动到线段 外时， 、 中有一个由正变负，所以上面的论证表明：

　　等腰三角形底边延长线上一点到两腰的距离的差为定值，即一腰上的高．

　　例2  中有两个内接矩形 ， ，都有一条边在 上，另两个顶点分别在 、 上（图4）．如果两个矩形的周长都是20，

　　1）求证任意一个一边在 上，另两个顶点分别在 、 上的矩形 的周长是20．

　　2）求 的面积．

　　解  以 为 轴， 点坐标为（ ，0），由于 与 到 的距离只差一个常数因子 ，所以 是 的一次式．这个一次式的 与 或 重合时，它的值都是10，因此这一次式是常数10．即矩形 的周长是20．

　　当 与 重合时，矩形退化为 上的高的两倍，所以这高为10．当 与 重合时，矩形退化为 的两倍，所以 为10．从而 的面积为50．

              

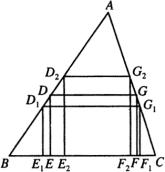
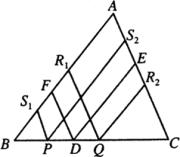
　　例3  在 的底边 上，有一条长为定值 的线段 在滑动．自 、 作 的平行线分别交 于 、 ，作 的平行线分别交 于 、 ．证明梯形 与梯形 的面积之和为定值（图5）．

　　证  设 为 的中点．作 ，交于 于 ．作 于 ．则 、 分别为梯形 、 的中线，而这两个梯形的高分别为 、 ．所以它们的面积之和

        　　　　　　　　　　　         　      

　　与前两个例题的推理相同，我们有

．

　　这里 是 的 边上高．于是

　　例4  （第二届全国中学生数学冬令营试题）．将边长为1的正三角形 的各边都 等分，过各分点作平行于其它两边的直线，将这个三角形等分成小三角形．各小三角形的顶点称为结点．在每个结点放置了一个实数．已知

　　（1） 、 、 三点上放置的数分别是 、 、 ．

　　（2）在每个由有公共边的两个小三角形组成的菱形之中，两组相对顶点上放置的数的和相等．

试求：

　　（1）放置最大数的点与放置最小数的点之间的最短距离 ．

　　（2）所有结点上的数的总和 ．

　　解  条件（2）可叙述成：在所述菱形中，两相邻顶点上放置的数的差与另两个相邻顶点上放置的数的差相等．

　　由此可知，下图中同一条线上的三个连续的结点上放置的数成等差数列（因为有两个结点既与这三个连续结点的前两个构成菱形，也与后两个构成菱形）．

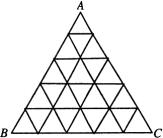
　　由于等差数列的每一项都是首项与另一项的一次式，所以各结点上放置的数都有是 、 、 的一次式．

　　如果 ，那么所放置的数均相等， ．如果 、 、 不等，设 最大， 最小．由于等差数列中，最大（最小）的项是首项或最末一项，所以在所放置的数中也是 最大， 最小． ．

　　现在考虑总和 ．它也是 、 、 的一次式．而且，当 、 、 中任意两个字母互换时，相当于改变三角形的位置，所以总和 保持不变，即 是 、 、 的对称式（对称函数）．因此 、 、 的系数相等，即

　　其中 、 为待定系数．

　　令 ，这时所有结点上的数为0， ．从而 ．

　　令 ，这时所有结点上的数为1， 等于结点的个数

　　从而

　　因此