第一节 不等式的性质

不等式的几个性质

　　不等式的性质是后继学习的基础，熟练掌握并能灵活运用不等式的性质，是提高解题准确性和快捷性的关键。这里介绍一些课本中没有直接列出而在解题中经常遇到的性质，以供参考。

1．乘方、开方性质

1）若 ，则有：

　　① ；

　　② 。

2）若 ，则 。

3）若 ，则 或 。

2．取倒数性质

1）若 或 ，则 。

2）若 或 ，则 。

3．取绝对值的性质

1） 。

2）若 ，且 ，①当 时，有 ；

3）当 时，有 。

4．有关分数的性质

　　若 ，且 ，则

1）真分数的性质：

　　① ；

　　② 。

2）假分数的性质：

　　① ；

　　② 。

　　说明：1）是真分数的性质，可简述为：真分数越加越大，越减越小。2）是假分数的性质，可简述为：假分数越加越小，越减越大。

　　以上性质都可由基本不等式或绝对值的定义，通过简单推导而得到，作为练习，其证明均留给读者。对以上不等式，建议大家熟练掌握，这对加快解题速度有帮助。

巧用不等式性质速求物理量极值

　　极值问题是物理应用中常见问题之一，解决这类问题的方法有几种，如二次函数配方法、二次方程判别法、三角函数法、几何作图法，对于同一问题采取方法不同，其效果往往并一样。如果一类问题，涉及到两个变量和为定值，求相应量极值问题，即定和求积觅极值。就可用不等式性质求极值，收到事半功倍的效果。

　　假设有变量 、 ，且 、 ，则一定有 ，

　　如果 （定值），则当 时， 有极大值为

　　例：如图1，粗细均匀的玻璃管长 厘米，开口向上竖直放置时，上端齐管口有一段 厘米的水银柱封闭着 空气柱，大气压强为 厘米汞柱，现使空气柱温度逐渐升高，问欲使管内水银全部溢出，温度至少升到多高？

　　　　

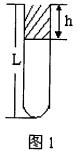
　　解：设管内空气柱温度升高到T（开），管内尚有水银柱 厘米，管的横截面积为S，则有

将数据代入，整理得：

如果再变为有关 的二次函数求极值，解答就较为复杂，由于 为常数，所以当 时，即当 厘米时，T有极大值为 （开）。

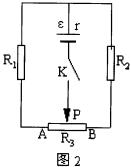
　　例2：如图2所示电路中，已知电源电动势 内阻 ，定值电阻 ， ， 是总阻值为 的滑动变阻器，闭合电键K，调节变阻触点，求通过电源的最小电流？

　　解： 、 、 与电源组成的电路实际上是双臂环路，

　　通过电源电流最小时，实际对应总电阻最大，设AP段阻值为X，那么：

　　由于 （定值），

　　所以当 时，即 时， 有最大值， ，因此通过电源电流

（A）

　　以上分析可看出，利用不等式性质求极值不失为一种好方法，我们不妨试一试。

中学数学授课的九种开头方式

常方平

　　教学方法 俗话说：“万事开头难”。想上好一堂数学课，有一个好的开头是很关键的。11年来，我一直努力地探索和试验着数学授课的开头，现总结九种中学数学授课的开头方法，与同行商榷。

　　1．发现法

　　它是根据中学生好奇的心理特点，一上课就给学生提供一定的材料，让学生充分发现和解决问题的一种方法。如，学习“空间两个平面的位置关系”时，可先让学生认真观察教室的墙壁、天花板、桌面、地面等之间的关系，积极发现了空间两个平面的两种位置关系。学生心理上有了满意感，使后面学习有饱满的精神。

　　2．研究法

　　它是根据中学生爱争论的心理特点，一上课就给学生一定的问题，让他们充分讨论的一种方法。如，学习“指数函数的性质”时，先用小黑板把函数 和 的图象挂出，让学生前后左右充分讨论这两种函数所具有的性质，使后面推广研究指数函数 的性质及应用，进展十分顺利。

　　3．反馈法

　　它是根据信息论的反馈原理，一上课就给学生提出一些问题，根据学生的反馈效果，给予肯定或纠正后引入新课的一种方法。如，学习“同角三角函数的基本关系式的应用”时，先向学生提问同角三角函数的八个基本关系式以及各个关系式的变形式，知道学生熟练记忆同角三角函数的关系式后，学习它在求值、化简、三角恒等式证明的应用顺其自然。

　　4．趣引法

　　它是根据中学生爱听故事的心理特点，一上课就以有趣故事开头的一种方法。如，学习“球冠”时，开头给学生讲这样一个故事：唐僧一行四人上西天取经，行至一个前不着村后不靠店的大山中，渴饿万分，让猪八戒去化缘，老猪在一个山沟里发现一大球型西瓜端起正要去吃，一妖怪一刀将西瓜刮去一部分，吓得它把手中的西瓜往头一扣，腾云逃回。孙悟空、沙僧看着猪八戒头上的西瓜，笑着说：“好一个球帽子“。球帽子就是球冠。接着叙述球冠，学生很容易接受。

　　5．类推法

　　它是利用学生已有的某种知识，一上课就由这种知识类似地推出另一种知识的方法。如，学习“孤度制”时，先让学生回忆角度制中角的化分单位的方法，再引入孤度制，学生十分容易理解。

　　6．实例法

　　它是根据中学生对周围事物易作直觉思维的特点，一上课就举出学生熟知的生活实例的一种方法。如，学习“二面角”时，先把一本书打开，让学生看到书两部分所成的角，对二面角有一个感性认识，使后面研究二面角很方便。

　　7．强调法

　　它是根据中学生对有意义的东西有兴趣的特点，一上课就叙述本课时的重要意义的一种方法。如，学习“复数”时，先强调：有一种新数，十八世纪以后，它就在数学、力学和电学中得到了应用，现在已成为科学技术中普遍使用的一种工具。它就是复数。然后由数的概念的推广引入复数，学生听得聚精会神。

　　8．设疑法

　　它是根据中学生爱追根求源的心理特点，一上课就给学生创设一些疑问的一种方法。如，学习“球的体积”时，先给学生提出：我们能不能利用前面柱、锥体的体积公式推出球的体积公式呢？将一个底面半径和高都等于球半径的圆柱，挖去一个以圆柱的上底面为底面、下底面圆心为顶点的圆锥，剩余的体积与半球的体积会相等吗？学生带着这样的疑问，使球的体积公式的推导十分顺利。

　　9．直接法

　　它是一上课就把要解决的问题提出来的一种方法。如，学习“三垂线定理”时，先把定理的内容板书在黑板上，让学生分清定理的条件与结论后，证明过程十分容易进展。

　　以上中学数学授课的九种开头方法的运用，一般是新概念学习课用发现法、研究法、趣引法、实例法、类推法，新定理学习课用设疑法、直接法，习题课及复习课用强调法、反馈法等。但根据学生的临课情况，可灵活变更授课的开头方法，象习题课及复习课有时也可用发现法、研究法、趣引法等。新概念学习课有时也可用强调法、反馈法等。

　　以上中学数学授课的九种方法，通过数年的试验，效果良好。如战前动员的力量，一席话能使千军万马群情振奋，所向披靡。学生在适当的授课开头作用下，学习积极性高，精神饱满，活动踊跃，听练主动。但，这九种方法一定有不足之处，望大家批评指正。

（摘自《中学数学参考》1991年第5期）