设为首页
设为首页
 加入收藏
加入收藏
扩展资料
中学数学应用问题与数学建模的差异研究
数学在日常生活中的广泛应用性已得到充分肯定和重视,数学应用问题已成为考查学生分析问题和解决问题的能力的重要途径.但数学建模与中学数学应用问题不完全是同一个问题,存在许多差异.值得中学师生注意和重视.
1 什么是数学建模
数学建模指根据具体问题,在一定假设下找出解决这个问题的数学框架、求出模型的解,并对它进行验证的全过程.
数学建模是一个“迭代”过程,每次“迭代”包括实际问题的抽象、简化,作假设明确变量与参数,形成明确的数学框架;解析地或数值地求出模型的解;对求解所得结果解释、分析和验证;如果符合实际可交付使用,如果与实际情况不符,需对假设作修改,进入下一个“迭代”.经过多次反复“迭代”,最终求得令人满意的结果.
2 建模的方法
数学的方法很多,但从理论上讲,主要有以下两种方法:
2.1 机理建模方法:利用物理、化学、生物学、经济学、社会学原理建立起数学模型的方法.
2.2 系统辨识建模方法:直接利用观察数据,根据一定的优良性准则在模型集中找出与数据拟合得最好的模型.这种方法在建立过程控制模型中是常用的.
3 数学建模的一般步骤
目前数学建模的教学理论尚未正式形成,然而数学建模的6个步骤却是所有建模教材的共同内容,也是学习数学建模者所必须掌握的内容.
3.1 建模准备.要求建模者深刻了解实际问题的背景,明确建模的目的,进行深入细微的调查研究,尽量掌握建模对象的各种信息和数据,找寻实际问题的内在规律.
3.2 作假设.现实问题涉及面广,数学模型不能面面俱到,应该把实际问题适当的简单化或理想化.这就必须作一定的假设,注意假设应该符合实际背景.
3.3 建立模型.根据问题的要求和假设,利用恰当的数学方法建立各种量之间的数学关系.建立数学模型时应使用何种方法,应视实际问题而定.如遇离散时间问题可以用处理离散问题的数学方法,如规划论、网络优化、马尔可夫链等,遇到连续的问题应用连续问题的数学方法,如微积分、微分方程、变分法、平稳过程等.一般地说,在建立数学模型时可能用到数学的任何一个分支,同一个实际问题还可以用不同方法建立不同的数学模型.当然,在达到预期目标前提下,应该采取尽可能简单的数学方法建立容易实现的数学模型,以便让更多的人接受和使用这种模型.
3.4 模型求解.包括求解各种类型的方程,大多数模型求解需要上计算机计算,求解还包括画图、列表和证明定理以及制作计算机软件等.
3.5 讨论和验证.根据模型的特点和模型求解结果,进行分析讨论,如算法的稳定性、精度影响.根据计算结果对问题作出解答、预测或提供最优决策和控制方案.最后将模型的结果与实际情况相比较,检验模型是否合理,说明模型的使用范围及注意事项.
3.6 模型的应用.把得到的数学模型应用到实际问题中去.
应该指出建立模型是一个过程,不是一种死板的步骤,如果在讨论和验证时发现模型确实合理,当然可将模型投入应用,如果发现模型不合理,那就必须修改,重新建模,重新求解,再作验证.这一过程可以循环往复,直到获得满意的结果为止.
4 中学数学应用问题与数学建模的差异
中学数学应用问题与数学建模都是为了培养学生应用数学解决实际问题的能力,从步骤上看也有许多相似之处.然而两者都有着层次上的差别,存在着质的差异.
4.1 中学数学应用问题是数学专家和命题者经过精心加工提炼出来的,问题比较明确,问题中给出的条件一般是充分的;而数学建模的问题直接来自实际,问题中的条件往往是不充分的,有时甚至要求同学自己动手来收集数据.
例如,1985年美国大学生数学竞赛的一个问题:建立一定的环境中动物自然生长的数学模型.一定环境指有限的食物、空间、水等等.选择一种你可以找到与环境有关数据的鱼或哺乳动物(如北美的小种马、兔子、鲑鱼、条纹鲈鱼等等),对于这种动物的总数建立数学模型并给出最优的饲养量.参赛队必须自己查阅资料,收集数据,才能完成问题的解答,这样的问题是在中学数学应用问题中不会出现的.
4.2 在数学建模过程中为了使问题更明确,作一定的假设是必须的;然而在解决中学数学应用问题时,一般不需要假设.
4.3 数学建模的讨论与论证,比解中学数学应用问题的验证要复杂得多.不仅要验证是否有增根或不符题意的根,而且还要考察它们与假设是否矛盾,与实际情况是否吻合等.
4.4 中学数学应用问题只要求写出答案,而数学建模需要写一篇报告文章来总结.
4.5 数学建模比中学数学应用问题更能贴近日常生活和生产实际,具有更高的科研价值.
5 中学数学应用问题与数学建模的差异给我们的反思
中学数学应用问题与数学建模的教学的影响是深远的,随着中学数学应用问题与数学建模的教学的逐步实施,数学知识应用竞赛的逐年开展,其深刻影响将逐步显现出来.
5.1 中学数学应用问题与数学建模的教学推动了数学教学改革.过去那种封闭式的,题海教学方式将受到越来越大的冲击,数学建模教学给中学数学应用问题教学指明了方向.数学建模教学要求学生掌握观察事物,归结数学问题的能力.这种能力的培养是与21世纪的科技发展相适应的,而且是必须的.一些渗透数学建模思想的试题也将逐步在各类升学考试中出现.这必将推动数学教材教法的改革.
5.2 中学数学应用问题与数学建模的教学是一种素质教育.相当多的学生对用数学解决实际问题,比做纯粹的数学题更有兴趣、更有积极性.参加数学建模竞赛的学生要求他们具有协作精神,能互相配合、克服困难,这正是现代科学研究中要求和提倡的团队精神.中学数学应用问题与数学建模的教学还能逐步培养学生作学问,善于思考的品质.越来越多的国内外数学教育工作者认识到:数学知识的真正掌握不是教出来的,而是在实践中实现的.中学数学应用问题的教学与数学建模正好是一个学数学、做数学、用数学的过程,它体现了学和用的统一.科学技术需要创新,数学教学也需要创新,而中学数学应用问题的教学与数学建模为学生提供了创新的环境和条件.1989年美国大学生“数学建模”竞赛中有这样一个试题:1981年发现了两类新的飞蚊,测得15个飞蚊的翼长和触角长数据,其中6个属于APF类,9个属于AF类,现在又得到3个新飞蚊,其翼长和触角长分别是(1.24,1.80),(1.28,1.84),(1.40,2.04),试问它们应属于哪一类?(三只新飞蚊的数据和原来15只飞蚊的数据都不重合).
通常人们都认为这是典型的统计判别分析问题.但是有一个参赛队将它作人工神位网络问题加以处理,结果和统计方法一样.评判委员会看不懂这队学生的答案,送给神经网络专家评议,结果大受赞赏,获得“杰出优秀论文奖”.学生的创新在数模竞赛中获得了特别嘉奖.
5.3 中学数学应用问题与数学建模所涉及到的问题都是与日常生活或科学技术相关的问题,是对学生数学、语文、外语、计算机运用能力的全面考核,这样打破了学科界限,为共同研究问题开了先河,对中学各科教学起了不可替代的作用,促进了学生的全面发展.
因此,中学教师的职前培训,很有必要开设数学建模课,在职后教育中继续学习并研究数学建模已经成为时代的要求.另一方面,通过对数学建模的学习和研究,能准确地把握中学数学应用问题的深度和难度,更好地推动了中学数学教学改革.
扩展资料
曲柄连杆机构的设计
 自动化中最常用的机构之一是曲柄连杆机构,它可使旋转运动与往复直线运动相互转化,下面我们介绍一种常见的曲柄连杆机构及其设计.
自动化中最常用的机构之一是曲柄连杆机构,它可使旋转运动与往复直线运动相互转化,下面我们介绍一种常见的曲柄连杆机构及其设计.
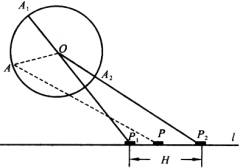
如图,主动机是曲柄OA,从动件是连杆AP与滑块P,机架、导轨l(不动件)如图组合而成,电动机带动曲柄旋转,通过连杆带动滑块在导轨上做往复直线运动.
设旋转中心O到导轨的距离为e,滑块的最大行程为H,滑块两极限位置
![]() 在O点所张的角为
在O点所张的角为
![]() (叫做极位夹角).当连杆
(叫做极位夹角).当连杆
![]() 与曲柄
与曲柄 ![]() 重叠时,滑块到达位置
重叠时,滑块到达位置 ![]() ;连杆
;连杆 ![]() 与曲柄
与曲柄 ![]() 成一直线时,滑块到达位置
成一直线时,滑块到达位置
![]()
在实际设计中,常常需从已知数据e,H,
![]() 出发,求出曲柄OA之长r,连杆AP之长x.下面我们来解决这一问题.
出发,求出曲柄OA之长r,连杆AP之长x.下面我们来解决这一问题.
在 ![]() 中,
中,
![]()
![]()
![]()
根据余弦定理,有
![]()
即
![]()
所以
![]()
又因为
![]()
所以
![]()
即
![]()
解由①,②构成的方程组,得
![]()
因为 ![]() 所以
所以