 设为首页
设为首页
 加入收藏
加入收藏
有趣的米勒问题
米勒(Johannes Miiller),德国数学家,曾在莱比锡、维也纳学习天文学和三角学,1468年至1471年在维也纳大学任教授,1471年定居纽伦堡,从事天文学研究,米勒对三角学做出了贡献.大约在1461至1464年间,他写成《论三角》书,书中给出了有关球面三角学的正弦定理、余弦定理、计算了三角函数表,相当精确.他的这些工作使三角学脱离文学而成为一门独立的学科.另外,米勒在研究几何时采用了代数方法,这在当时是别具一格的.
1471年,米勒向诺德尔(Christian Roder)教授提出以下十分有趣的问题:
在地球表面的什么部位,一根垂直的悬杆呈现最长?(即在什么部位,可见角为最大?)
在米勒的家乡哥尼斯堡,这个问题称为雷奇奥莫塔努斯(Reqiomontanus)的极大值问题.该问题本身并不难,然而作为载入世界数学史上的第一个极值问题而引人注目.
下面这个简明解法是罗斯(Ad·Lorsch)给出的.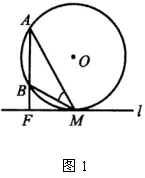
如图1,设 ![]() 为杆的上端点,
为杆的上端点, ![]() 为杆的下端点.
为杆的下端点. ![]() 垂直于地平面,垂足记为
垂直于地平面,垂足记为 ![]() ,于是线段长
,于是线段长 ![]() ,
, ![]() 均为已知,以
均为已知,以 ![]() 为中心在地球表面上画的圆上的所有对
为中心在地球表面上画的圆上的所有对 ![]() 的视角都相等.因此,我们只需过
的视角都相等.因此,我们只需过 ![]() 任作一条垂直于
任作一条垂直于 ![]() 的直线
的直线 ![]() 并在这条水平地沿着地球表面的线上找出这样的点
并在这条水平地沿着地球表面的线上找出这样的点 ![]() ,使得在这点的可见角
,使得在这点的可见角 ![]() 最大.
最大.
△ ![]() 的外接圆
的外接圆 ![]() 必与
必与 ![]() 相切干
相切干 ![]() 点.事实上,若
点.事实上,若 ![]() 不与圆
不与圆 ![]() 相切,则除
相切,则除 ![]() 点儿圆
点儿圆 ![]() 与
与 ![]() 还有另一个公共点
还有另一个公共点 ![]() ,而对于线段
,而对于线段 ![]() 的中点
的中点 ![]() 而言,
而言, ![]() 是圆
是圆 ![]() 的圆内角,这时,
的圆内角,这时,![]() ,这就与
,这就与 ![]() 是最大可见角矛盾.
是最大可见角矛盾.
设过 ![]() 的圆
的圆 ![]() 与直线
与直线 ![]() 相切于点
相切于点 ![]() ,则
,则 ![]() 取得最大值.这是因为对
取得最大值.这是因为对 ![]() 上异于
上异于 ![]() 的任一点
的任一点 ![]() 而言,
而言, ![]() 是圆
是圆 ![]() 的圆外角,所以
的圆外角,所以 ![]() .
.
![]() 点的位置可以这样来确定,根据切割线定理,
点的位置可以这样来确定,根据切割线定理,
![]() ,即有
,即有 ![]() .
.
从而,我们得出结论:以是杆与地面垂直的垂足为圆心,以是杆两端到地面距离的乘积的算术根为半径,在地球表面上画圆,该圆周上的点对悬杆的视角为最大.
1986年全国高考数学试题理科第五大题其实就是“米勒问题”: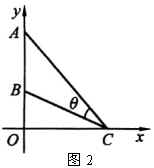
如图2,在平面直角坐标系中,在 ![]() 轴的正半轴(坐标原点除外)上给定两点
轴的正半轴(坐标原点除外)上给定两点 ![]() ,
, ![]() .试在
.试在 ![]() 轴的正半轴(坐标原点除外)上求点
轴的正半轴(坐标原点除外)上求点 ![]() ,使
,使 ![]() 取得最大值.
取得最大值.
下面,我们运用高中数学知识结出这道高考题的一种简洁解法.
解 如图3,设点 ![]() 的坐标为
的坐标为 ![]() ,点
,点 ![]() 的坐标为
的坐标为 ![]() ,
, ![]() ,
, ![]() 的坐标为
的坐标为 ![]() ,
, ![]() ,并记
,并记 ![]() ,
, ![]() ,
, ![]() ,则
,则 ![]() ,且
,且 ![]() .
.
所以 ![]()
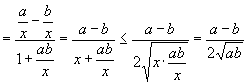 .
.
因此,当 ![]() ,即
,即 ![]() 时,
时, ![]() 取得最大值
取得最大值 ![]() .
.
因为在 ![]() 内
内 ![]() 是增函数,所以当
是增函数,所以当 ![]() 时,
时, ![]() 取得最大值
取得最大值 ![]() .故所求的
.故所求的 ![]() 点坐标为
点坐标为 ![]() .
.
更一般的“米勒问题”(解略)是:
在已知直线 ![]() 的同侧有
的同侧有 ![]() ,
, ![]() 两点,试在
两点,试在 ![]() 上求一点
上求一点 ![]() ,使
,使 ![]() 最大.
最大.
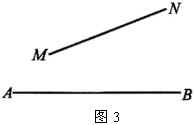
将此问题特殊化,便可得到1984年西安市中学生数学竞赛试题:
在直线 ![]() 上求点
上求点 ![]() (如图3),使
(如图3),使 ![]() 对线段
对线段 ![]() 有最大视角,证明你的结论.
有最大视角,证明你的结论.
(原载《数学通讯》2000年第22期,宋庆文)