第三节 解直角三角形

扩展资料

怎样求折痕的长？

　　在代数、几何中经常遇到需求折痕长的习题，不少学生由于对折痕的特征不甚了解，因此往往束手无策．

　　比如有这样一道题：

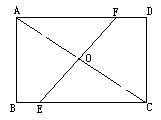
　　如图，已知：四边形ABCD是矩形，AB=3，BC=4，把矩形折起，当点C与点A重合时，折痕为EF．试求：EF的长．

　　事实上，由于EF是点C与点A重合时的折痕，因此EF是线段AC的垂直平分线．
　　
　　如能注意到利用已知可求得tg∠FAO,则在Rt△AFO中，根据tg∠FAO=FO/AO，FO即可求得，从而EF的长也易求得。（也可利用Rt△AOF∽Rt△ADC，得到：FO∶AO=CD∶AD，从中求出FO．)

　　解 连接AC，与EF相交于点O．

　　∵四边形ABCD是矩形，

　　∴∠FAO=∠ECO．

　　又∵EF垂直平分AC，

　　∴OA=OC，∠AOF=∠COE(=90°)，
　　
　　∵CD=AB=3，AD=BC=4，
　　
　　
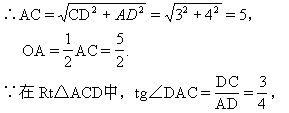
　　感兴趣的同学不妨考虑一下怎样解下面一题：

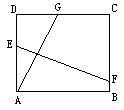
　　如图，已知：四边形ABCD是正方形， AD=12cm， DG=5cm．把正方形折起，当点A与点G重合时，折痕为EF．试求：EF的长．(答案：EF=13cm)

返回页首