第八节 反比例函数及图象

扩展资料

马尔克广场上的游戏

　　在世界著名的水都威尼司斯，有个马尔克广场.广场的一端有一座宽82米的雄伟教堂.教堂的前面是一方开阔地.这片开阔地经常吸引着四方游人到这里做一种奇特的游戏：把眼睛蒙上，然后从广场的一端向另一端教堂走去，看谁能到达教堂的正前面！

　　奇怪的是，尽管这段距离只有175米，但却没有一名游客能幸运地做到这一点！全都如下图那般，走成了弧线，或左或右，偏斜到了一边！

　　类似的情形也有很多，这与俗话说的鬼打墙类似.有许多人在沙漠或雪地里，由于迷失方向而在原地打圈子，这一切近乎玩笑般的遭遇，终于引起了科学家的注意.

　　公元1896年，挪威生理学家古德贝对闭眼打转的问题进行深入的探讨.他搜集了大量的事例后分析说：这一切都是由于人自身两条腿在作怪！长年累月养成的习惯，使每个人一只脚伸出的步子长一段微不足道的距离.而正是这一段很小的步差x，导致了这个人走出一个半径为y的大圈子！

　　现在我们将这个过程数学化，研究一下x与y之间的函数关系.

　　假定某个两脚踏线间相隔为d.很显然，当人在打圈子时，两只脚实际上走出了两个半径相差为d的同心圆.设该人平均步长为1.那么，一方面这个人外脚比内脚多走路程

　　

　　另一方面，这段路程又等于这个人走一圈的步数与步差的乘积，

　　即： 　　

　　对一般的人， 米， 米，代入得（单位米）

　　

　　这就是所求的迷路人打圈子的半径公式.是我们学过的反比例函数(图象如下图).今设迷路人两脚步差为 毫米，仅此微小的差异，就足以使他在大约三公里的范围内绕圈子！

　　让我们回到那个马克尔广场的游戏上来.我们先计算一下，当人们闭起眼睛，从广场一端中央的M点，要想抵达教堂CD，最小的弧线半径应该是多少？

　　如图，注意到矩形ABCD边BC=175（米）， （米）．上述问题可以转化成几何中的命题：已知 与 ．求 的半径 的大小．

　　

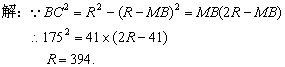
　　这就说,游人要想成功,他所走弧线半径必须不小于394米．我们再来计算一下，要达到上述要求，游人的两脚步差需要什么限制．

　　

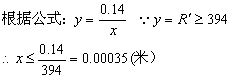
　　这表明游人的两只脚步差必须小于 毫米，否则就难以成功．然而在闭眼的情况下两脚这么小的步差一般人是达不到的，这就是在游戏中为什么没有人能够蒙上眼睛走到教堂前面的道理．

返回页首