第四节 一元二次方程的根与系数的关系

扩展资料

　　1.如何从反面提出问题推导一元二次方程根与系数的关系？

　　答：可以这样进行．

　　已知方程ax²＋bx＋c＝0，变形为

　　

　　依求根公式得它的两根为

　　

　　可见，一元二次方程的根是由它的系数确定的．

　　反过来，如果已知一元二次方程的两个根x₁、x₂能否确定它的系数呢？回答是肯定的．

　　 ∵x₁、x₂是方程的两个根

　　 ∴(x－x₁)(x－x₂)＝0

　　∴x²－(x₁＋x₂)x＋x₁x₂＝0

　　

　　比较两式可得：

　　

　　解答提示：这是用逆向思维的方式从反面提问题，是符合人们的思维规律的．当一个定理被得到证明后，人们立即会想到它的逆命题是否是真命题？一元二次方程根的判别式，根与系数的关系都是可逆的．

　　二次项系数是1的一元二次方程的一般式为

　　x²＋px＋q＝0

　　它的两根为x₁、x₂，

　　那么

　　x₁＋x₂＝－p x₁x₂＝q

　　这是经常被用到的．

　　2. 不解方程，能直接求出有关根的代数式的值吗？

　　在教材中介绍了利用一元二次方程根与系数的关系(韦达定理)，可以不解方程,

　　现有下述这道习题：

　　已知：一元二次方程ax²＋bx＋c＝0(a≠0)的两个根分别为x₁、x₂，不解方

　　

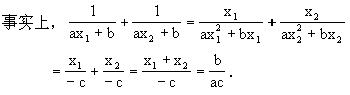
　　3.求作一元二次方程的又一方法

山东省博兴县实验中学（256500）  毛会基

　　四年制初中代数第三册第36页B组，是求作一个一元二次方程，使它的两根与已知方程两根之间有特定的关系的题目。

　　原题  已知方程，利用根与系数的关系求一个一元二次方程使它的根是原方程各根的（1）平方；（2）相反数；（3）3倍；（4）倒数。

　　一般常用方法是利用根与系数之间的关系，确定新方程的一次项系数、常数项来得到二次项系数为1的一元二次方程的。

　　有没有其他的方法呢？既然两个方程的两根之间有特定的关系，我们可以直接利用根的定义来求作新的方程，看下面的解题过程：

　　①解  设所求的方程的根为y，则有

　　即，这样代入原方程，得

　　

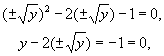
　　。两边平方得

　　

　　得  ，即是所求的方程。

　　②解  设所求方程的根为y.

　　则  即  ，

　　代入原方程得

　　   

　　求得新方程。

　　③、④解题过程略。

　　类似地，我们可以求各根是原方程各根的平方、倍数（几分之几）、比各根大几（小几）等的一元二次方程，只要一个方程与原方程各根之间有直接的关系，那么我们就可以用这种方法得到。

　　本文介绍的方法，是直接利用根的定义得到新方程。思路清晰，步骤简捷，过程简便，解法巧妙。体现了解数学题过程中的灵活性和趣味性。

返回页首