第十二节 等腰三角形的性质

扩展资料

谈谈斯坦纳——雷姆斯定理

湖南沅江市白沙公机关 万喜人

　　1840年，雷姆斯(C.Lehmus)向著名几何大师瑞士人斯坦纳(J.Steiner)提出了一个看起来十分简单的几何问题，要求给以证明．问题是：

　　命题 三角形两个底角平分线相等便是等腰三角形．

　　斯氏答应研究它，但他直到1844年才发表定理的征明．后来该命题就以斯坦纳—雷姆斯定理而闻名于世．150多年来，经常有论述它的文章发表．笔者见过斯—雷定理的证明30余种，比较而言，觉得还是以斯氏原证为佳．

　　问题 在△ABC中，∠B、∠C的平分线分别为BD，CE，且BD=CE．求证：AB＝AC．

　　斯坦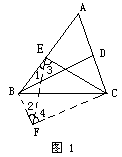纳原证 如图1，假设AB＞AC．

　　则∠B＜∠C，从而∠BEC＞∠BDC(1)

　　在△BCE与△CBD中，

　　∵BD=CE，

　　BC公共，∠BCE＞∠CBD，

　　∴BE＞CD．

　　作平行四边形BDCF，连接EF．

　　∵BE＞CD=BF．∴∠1＜∠2．

　　∵CE=BD=CF ．∴∠3=∠4．

　　∴∠BEC＜∠BFC=∠BDC (2)

　　(1)与(2)矛盾．∴AB≯AC．

　　同理AC≯AB．故 AB=AC．

　　之所以说斯氏原证好，是因为它不仅简洁优美，而且另一些证明三角形等腰的问题也可仿照斯氏原证证明．请同学们看以下三例．

　　例1 如图2，在△ABC中，AT⊥BC于T，垂足T在BC上，H为垂心，P为HT上任意一点，将BP交 AC于D，CP交AB于E，且BD=CE．求证：AB=AC．

　　证明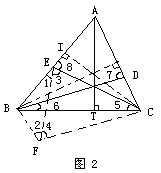：假设AB＞AC，则BT＞CT，BP＞CP，∠5＞∠6．在△BCE与△CBD中，

　　又因CD=BD，BC公共，

　　∴BE＞CD．

　　设CH⊥AB于I，BH⊥AC于K．

　　在Rt△CIE与Rt△BKD中，

　　∵CE=BD，由AB＞AC，知CI＜BK，

　　∴∠8＜∠7．

　　∴∠BEC＞∠BDC (1)

　　作平行四边形BDCF，连接EF，

　　∵BE＞CD=BF，∴∠1＜∠2．

　　∵CE=BD=CF，∴∠3=∠4．

　　∴∠BEC＜∠BFC=∠BDC(2)

　　(l)与( 2)矛盾．∴AB≯AC．

　　同理AC≯AB．故AB=AC．

　　

　　例2 在△ABC中，点M，N分别在AB，AC上，AM=AN．D，E分别为NC，MB的中点，且 BD=CE．求证：AB=AC．

　　证明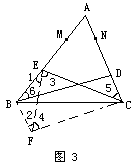：如图3，假设AB＞AC，则BE＞CD，AE＞AD．

　　

　　∴sin∠5＞sin∠6．

　　但0°＜∠6＜90°，

　　0°＜∠5＜180°，

　　∴∠5＞∠6．从而∠BEC＞∠BDC (1)

　　作平行四边形BDCF，连接EF．

　　∵BE＞CD=BF，∴∠1＜∠2

　　∵CE=BD=CF，∴∠3=∠4．

　　∴∠BEC＜∠BFC=∠BDC．(2)

　　(1)与(2)矛盾．

　　∵AB≯AC．

　　同理AC≯AB．故AB=AC．

　　例3 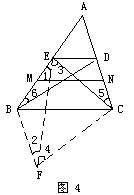在△ABC中，点M，N分别在AB，AC上，BM=CN．点D，E分别在AN，AM 上，且DE∥MN，BD=CE．求证：AB=AC．

　　证明：如图4，假设AB＞AC，则AM＞AN．

　　又DE∥MN，

　　∴AE＞AD，

　　EM＞DN，BE＞CD．

　　

　　∴sin∠5＞sin∠6

　　但0°＜∠6＜ 90°．

　　0°＜∠5＜180°，

　　∴∠5＞∠6．从而

　　∠BEC＞∠BDC．(1)

　　作平行四边形BDCF，连接EF．

　　∵BE＞CD=BF，

　　∴∠1＜∠2．

　　∵ CE=BD=CF，

　　∴∠3=∠4．

　　∴∠BEC＜∠BFC=∠BDC．(2)

　　(1)与(2)矛盾．∴AB≯AC．

　　同理AC≯AB．故AB=AC．

　　下面是斯—雷定理的两个推广，也可仿照斯氏原证证明．留给同学们作为练习．

　　2．在△ABC中，D，E分别是AC，AB上的点．BD与CE相交于P，若

　　

返回页首