第七节 角的画法

扩展资料

浅议平面几何的语言教学

　　掌握几何语言是正确认识图形性质，顺利进行逻辑推理的必要条件．对初二学生来说，熟练掌握几何语言是有一定困难的．学生在语言表达上的困难，往往超过一般教师的估计．如用三个大写字母表示一个角时，常常不会把顶点字母放在中间，用顶点字母表示一个角时又往往表示了其中一个分角；作AB的平行线时不说过AB外的什么点，作圆和弧也不说以什么为圆心，以什么为半径等．对此，教师应有充分估计，在教学中不能急躁，要循序渐进．下面谈四点体会：

　　首先要使学生透彻理解几何术语所反映对象的意义，把几何语言与图形、数学符号紧密结合起来．如开始时，学生对于“任意一点”，“每两点”，“互相”（平分，垂直），“反向延长”，“顺次截取”，“有且仅有”等这些用语不甚理解，不会运用．针对这种现象在教学中对于每一个新出现的术语，都必须讲清其意义，结合图形使学生透彻理解．比如“线段AB与CD互相平分”是指AB与CD相交，有一个交点设为O，且AO=BO与CO=DO同时成立，如图1．而图2中虽有AB与CD相交，且AO=BO，但CO≠DO，所以不能称AB与CD互相平分，而可称线段CD平分线段AB．

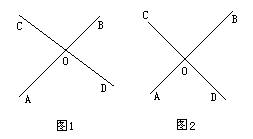
　　2．教师使用的语言要与课本上表述的语言相一致，做到语言规范化．因为教师的口语与板书无时不在影响着学生，所以教师语言的示范作用不能忽视．教师不要把学生尚未学过的词语带到教学中来，以免产生不必要的教学困难．如在讲了两条直线垂直后提出问题：OD是∠AOC的平分线，OE是∠COB的平分线，问OE与OD是什么位置关系？由于尚未研究两条直线的“位置关系”，学生会由于不懂“位置关系”这一词语而选成解题困难，这样的困难完全是由于教师语言疏忽而产生的．

　　教师语言的规范化，并不排斥教师在不失科学性的前提下采用较为通俗、浅显的直观语言对学生进行启发、引导，进行较为抽象的几何对象的数学．

　　对于几何命题的数学，还要经常性地从语法角度进行剖析，分清层次．如等量公理中的“等量的同分量相等”的教学，可以结合图形——两线段或两角，先讲清什么叫等量，再讲什么叫等量的同分量，最后得出“等量的同分量相等”的结论．

　　3．加强学生几何语言的训练，努力提高学生的说理能力．课堂数学要形式多样，有讲有练，给学生较多的语言训练机会．如要求学生复述定义、定理的意义；教师给出图形，要求学生“看图说话”讲述意义；教师写出各论证，要求学生说出根据，理由等．

　　语言训练中逐步要求学生做到语言精练，表述正确，对于学生模糊不清的口语，要一一加以纠正，毫不放松．语言训练要重视课本的作用．教学中要引导学生看书，同时对于一些语言程式和习惯用语，如“连结××并延长交××于×点”“延长××到×，使××等于××”等，可以要求学生熟记，以利于熟练地掌握和正确地使用几何语言．

　　适当的反例教学可以提高学生使用语言的精确性．如教学中经常让学生来辨析诸如下列一类的语句：“到一条线段两端距离相等的点是线段的中点”，“两条线段不平行就相交”；“过线段AB外一点作AB的垂线”；“过M、N两点作直线AB的平行线”等等．

　　4．注意对几何语言进行整理小结，通过归类、对比等手段使学生掌握的几何语言系统化．比如，带有“任意”的几何语言有：在直线L上任取一点；以已知点为圆心，任意长为半径画弧；过A点任意作一条直线，过三点中的任意两点作直线等等．又如关于“存在与唯一性”的几何语言有：经过两点有且只有一条直线；过一点有且只有一条直线与已知直线垂直；过一点有且只有一条直线与已知直线平行；两条直线相交只有一个交点等等，这样不但整理了几何语言，同时也小结了有关基础知识．

　　只要我们从学生的实际出发，加强教师自身的语言修养，讲究教法，重视对学生的语言训练，并持之以恒，就能逐步使学生获得规范的几何语言，并能运用自如．

返回页首