第六节 角的度量

扩展资料

钟面上三针成等角问题

　　关于时钟的应用题是比较常见的，有些极具趣味性．从图形美的角度出发，如果钟面上时针、分针、秒针能两两成120°角，那是极为理想的情形．下面就来研究“钟面上三针能否两两成120°角？”

　　1．问题假设 三针是连续匀速转动的（即不是跳动），时钟是精确无误的．

　　2．等价叙述 钟面上时针、分钟成120°角时，秒针是否恰为其外角平分线？

　　3．特殊情形 当4时整、8时整，时针与分针成120°角，但此时秒针与分针重合，不合要求．

　　4．问题猜想 时钟的时针与分针从重合状态开始运动到下一次重合为止，共有两次成120°角，由于0至12时期间（半开区间（0，12））时针与分针共发生11次重合，因此有22次两针成120°角．当每次时针与分钟成120°角时，秒针的位置已经确定，秒针与时针、分针各成120°角机会不多．

　　5．问题解决 以钟面上“分”的刻度（共60个）来刻划三针的位置．

　　方法一 设x时y分时时针与分针成120°角，则由题意得

　　（p=或±1或±2，0≤x＜12，0≤y＜60，x∈N^＋）

　　也就是说，在12小时之内时针与分针成120°角的22次中y可表示为

　　实际上经冗举知q遍历0，1，2…，10，并且各取两次．

　　角，则方程

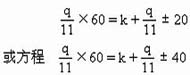
　　有整数解，即方程

　　有整数解．

　　由于（3）（4）中q=0，此时y为整数，又由（1）知60|y，y=0，此时分针与秒针重合，不合要求，故此问题无解．

　　方法二 时针、分针、秒针的转速分别为5格/小时、60格/小时、3600格/小时，从0时整开始，x小时后时针、分针、秒针分别转了5x格、60x格、3600x格，0≤x＜12．

　　三针两两成120°角，有两种情况．

　　（1）当时针、分针、秒针呈顺时针方向排列时

　　（2）当时针、分针、秒针呈逆时针方向排列时

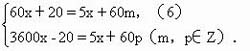
　　由（5）消去x得 3（719n－11q）=－730（7）

　　由（6）消去x得 3（719m－11p）=730（8）

　　因为3 730，故（7）（8）都不成立，即本题无解．

　　6．改变条件 （根据钟表的实际设计情况）

　　（1）如果时针、分针连续匀速运动，秒针每秒跳动一格（跳动时间忽略不计，以下同）．由上面方法一的讨论可知，若某一时刻三针符合条件，则时针与分针也刚好在整数格刻度处，从而秒针必在“0”刻度处，这显然是不可能的．本题也无解．

　　（2）如果时针连续匀速运动，分针每分钟跳动一格，秒针每秒钟跳动一格．与上面（1）的讨论类似，本题仍然无解．

　　秒跳动一格．如果某一时刻三针互成120°角，则三针都在整数格刻度处．当时针在整数格刻度处时，分针恰好处于“0”，“12”，“24”，“36”，“48”刻度上，要使时针与分针成120°角，则时针要处于“20”和“40”“32”和“52”“4”和“44”“16”和“56”“28”和“8”刻度处．经验证，分针处于“0”刻度处，时针处于“20”和“40”刻度处是可以的，此时钟面显示的符合条件的时间为4时40秒和8时20秒，根据针的跳动规律，钟面显示4时40秒表示的时间t的范围是：4时40秒≤t1＜4时41秒，钟面显示8时20秒实际表示的时间t2的范围是：8时20秒≤t2＜8时21秒．

　　综上所述，当三针连续匀速转动时，本题无解；当时针、分针匀速转动；秒针每秒跳动一格时，本题无解；当时针匀速转动，分针每分跳分针每分钟跳动一格，秒钟每秒跳动一格时，在两段时间内三针两两成120°角，即4时40秒≤t1＜4时41秒和8时20秒≤t2＜8时21秒．

返回页首