设为首页
设为首页
 加入收藏
加入收藏
技巧法求合力
在物理教学中,让学生系统地学习传统而又正规的解题思想和方法是必要的,尤其对初学者而言.但是,教学实践又告诉我们,若过分强调传统、正规的解题思想和方法,往往会使学生的思路单一、思维呆板;相反,适当地、有目的地介绍一些巧妙的解题思想和独特的解题方法和技巧,却能有效地提高学生的学习兴趣,开拓学生的思路,贯通学生的知识,培养和提高学生的创造性思维能力.一句话,能有效地提高学生的科学素养.下面我们将要介绍给读者的是三种求解合力的巧妙方法和独特思想,颇有趣味,望读者能领悟其中的精华,达到举一反三的目的.
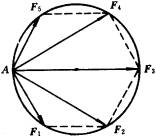
(1)设有五个力作用于一点A.这五个力的大小和方向,相当于边长为a的正六边形的两条邻边和三条对角线,如图所示.试求这五个力的合力.
力是矢量,矢量的合成遵循平行四边形法则.因此,按通常的解法本题的求解要用平行四边形法则来分析和讨论.具体方法可以用力的平行四边形法则和由平行四边形法则发展而得的力多边形法则两种.
但是,因为力矢量是用有向几何线段来表示的,故倘若借助于有关的几何定理,本题还可以有更巧妙的解法.
在图中,由题设条件可知, ![]() 是一个正六边,它有一个外接圆,
是一个正六边,它有一个外接圆, ![]() 是外接圆的直径.根据正六边形的几何性质,若它的边长为a,则其外接圆的直径必为2a.也就是说,力
是外接圆的直径.根据正六边形的几何性质,若它的边长为a,则其外接圆的直径必为2a.也就是说,力
![]() 的大小等于2a.
的大小等于2a.
从图中分析还可知,
![]() 构成一个平行四边形(实为矩形),从而得知
构成一个平行四边形(实为矩形),从而得知 ![]() 与
与 ![]() 的合力跟有向线段
的合力跟有向线段 ![]() 重合.这就是说,它们的合力的方向、大小跟
重合.这就是说,它们的合力的方向、大小跟 ![]() 完全一致.该合力的大小等于2a.
完全一致.该合力的大小等于2a.
同理,可以知道 ![]() 与
与 ![]() 的合力的方向、大小也跟
的合力的方向、大小也跟 ![]() 完全一致.该合力大小等于2a.
完全一致.该合力大小等于2a.
因此,可以确定,本题所给定的五个力的合力R,方向跟 ![]() 这个力一致,大小是这个力的3倍,即合力
这个力一致,大小是这个力的3倍,即合力 ![]() .
.
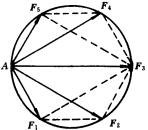
上述解法,由于充分利用了题目中“正六边形”这个几何条件,把力合成的矢量性,自然而又巧妙地同几何定理结合起来,使整个求解过程显得既简捷又巧妙.另外,从求解过程亦可看出,本题是一个数理结合的好例子.最后必须指出,上述巧妙解法,其理论依据仍是矢量合成的平行四边形法则,只不过是在求解过程中利用了几何定理,灵活运用力的平行四边形法则罢了.
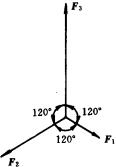
(2)如图所示,三个共点力,互成120°角.设 ![]() ,求这三个力的合力.
,求这三个力的合力.
本题若按常规解法,就得先求出两个力的合力,再求此合力和第三个力的合力.而合力的计算要用到余弦定理和正弦定理,并且要重复两次,较麻烦.如利用“三个互成120°角的相等的力的合力为零”的性质,可将上题的解法大为简化.
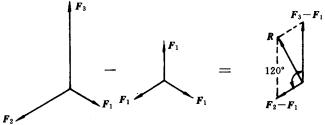
如图所示,把互成120°角的三个力 ![]() 在各自的方向上减去
在各自的方向上减去 ![]() ,其结果是不会改变合力的大小和方向的(平衡力的性质).这样一处理,就可把三力合成问题简化为两力合成问题(这里
,其结果是不会改变合力的大小和方向的(平衡力的性质).这样一处理,就可把三力合成问题简化为两力合成问题(这里 ![]() ,夹角为120°).
,夹角为120°).
所以,合力R的大小为:

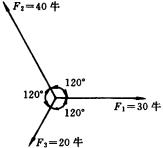
(3)20N、30N和40N的三个力作用于物体的同一点,它们之间的夹角都是120°,如图所示,求合力的大小和方向.
本题是求三个力的合力,由于所给的三力互成120°,有一定的对称性,故完全可像第(2)种方法一样求解,但我们不想重复,拟另辟捷径.
众所周知,力是矢量,可用有向线段表示.联想到复数与平面上的点有—一对应关系,平面上的点又与从原点出发的有向线段(向量)有—一对应关系,这就自然地启发我们把力和复数联系起来.
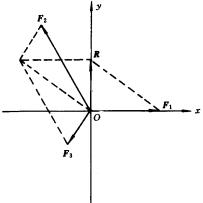
以力 ![]() 的方向为x轴的正方向,三个力的共同作用点为坐标原点,建立复平面坐标系(如图所示).
的方向为x轴的正方向,三个力的共同作用点为坐标原点,建立复平面坐标系(如图所示). ![]() 的复数的三角形式分别为:
的复数的三角形式分别为:
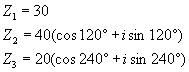
则求 ![]() 的合力R就是求这三个复数的代数和.所以,有:
的合力R就是求这三个复数的代数和.所以,有:
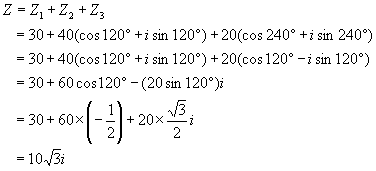
![]() 表示这个复数的向量在y轴的正半轴上(如图中的R),也就是说,合力R的方向与
表示这个复数的向量在y轴的正半轴上(如图中的R),也就是说,合力R的方向与 ![]() 的夹角为30°,R的大小为
的夹角为30°,R的大小为 ![]() 牛顿.
牛顿.
用复数表示力,是建立在力的矢量性基础上.一个复数对应着一个具体的力,通过这种对应,求几个共点力的合力就可以化为求几个复数的和.因为复数的求和只牵涉代数量的求和,所以通过复数就能把一个求矢量和的问题转化为求代数和的问题.关于这点,上述解法已经体现.力矢量可以如此,其他所有矢量求和,当然亦能如此.所以上述复数方法对矢量是通用的.应注意的是,把矢量表示成相应复数时,幅角一定要找准.另外,须强调一点,“对应关系”决不是“相等关系”,复数不是矢量本身,而只是它的某种运算符号.符号本身都有自己的运算法则,矢量也有自己的运算法则,重要的是由于这些运算法则满足一定的对应关系.在运算以后,我们还需反过来利用对应关系从结果中找出矢量本身.
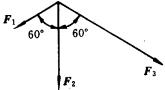
(4)三个共点力,如图所示, ![]() 与
与 ![]() 、
、 ![]() 皆成60°,求它们的合力.
皆成60°,求它们的合力.
不妨设 ![]() 中
中 ![]() 值最小.采用题2方法,即用“减法”,详见图.(因为
值最小.采用题2方法,即用“减法”,详见图.(因为 ![]() 减去反向的
减去反向的 ![]() 就得到
就得到 ![]() ),同样可把问题归结为计算两力的合力.具体计算从略.
),同样可把问题归结为计算两力的合力.具体计算从略.
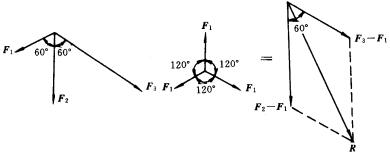
本题的解法技巧是第(2)种方法的发展和变通.
力的多边形定则
选自《中学教学实用全书》
力的多边形定则是共点力系合成的一种几何作图法.作图方法是:共点力系 ![]() 、
、 ![]() 、
、 ![]() 和
和 ![]() 合成时,可先按
合成时,可先按 ![]() 的大小和方向图示有向线段
的大小和方向图示有向线段 ![]() ,再以B端为起点按
,再以B端为起点按 ![]() 的大小和方向图示有向线段
的大小和方向图示有向线段 ![]() ,接着以C端为起点按
,接着以C端为起点按 ![]() 的大小和方向图示有向线段
的大小和方向图示有向线段 ![]() ,最后以D端为起点按
,最后以D端为起点按 ![]() 的大小和方向图示有向线段
的大小和方向图示有向线段 ![]() ,连接由A指向E的有向线段
,连接由A指向E的有向线段 ![]() 即表示该共点力系
即表示该共点力系 ![]() 、
、 ![]() 、
、 ![]() 和
和 ![]() 的合力F(如图所示).这种共点力系合成的作图法称为力的多边形定则.
的合力F(如图所示).这种共点力系合成的作图法称为力的多边形定则.
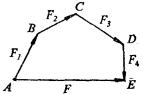
运用此种作图法确定共点力系的合力时,与图示力系中各力的先后顺序无关.
力的平行四边形法则
选自《中学教学实用全书》
共点力的合成法则.这一法则通常表述为:以表示两个共点力的有向线段为邻边作一平行四边形,该两邻边之间的对角线即表示两个力的合力的大小和方向.
由力的平行四边形法则可知,两个共点力的合力不仅与两个力的大小有关,且与两个力的夹角有关.当两个力的大小一定时,其合力的大小将随两个力夹角的改变在两个力之和与两个力之差范围内变化.
运用平行四边形法则求一共点力系的合力时,可采用依次合成的方法.例如求三个共点力 ![]() 、
、 ![]() 和
和 ![]() 的合力,可先求出
的合力,可先求出 ![]() 和
和 ![]() 的合力
的合力 ![]() ,然后再求出
,然后再求出 ![]() 和
和 ![]() 的合力
的合力 ![]() ,
, ![]() 即为三个共点力的合力.
即为三个共点力的合力.
平行四边形法则不仅是共点力的合成法则,也是一切矢量合成共同遵循的法则.
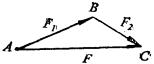
力的三角形定则
选自《中学教学实用全书》
两个共点力合成的一种几何作图法.作图方法是:两个共点力 ![]() 和
和 ![]() 合成时,可先按
合成时,可先按 ![]() 的大小和方向图示有向线段
的大小和方向图示有向线段 ![]() ,再以B端为起点按
,再以B端为起点按 ![]() 的大小和方向图示有向线段
的大小和方向图示有向线段 ![]() ,连接由A指向C的有向线段
,连接由A指向C的有向线段 ![]() 即两个共点力
即两个共点力 ![]() 和
和 ![]() 的合力F(如图所示).这种共点力合成的作图法称为力的三角形定则.
的合力F(如图所示).这种共点力合成的作图法称为力的三角形定则.