第四节 万有引力定律在天文学上的应用

关于重力的相关知识

一、地球上的重力和重力加速度

　　在质量为 、半径为 的天体表面上，如果忽略天体自转的影响，质量为 的物体的重力加速度 ，可以认为是由天体对它的万有引力产生的．由万有引力定律和牛顿第二定律有：

　　则该天体表面的重力加速度为：

　　由此式可知，天体表面的重力加速度是由天体的质量和半径决定的．

　　因为地球是一个极半径比赤道半径略小的椭球体，因而物体位于赤道上时，地球对它的引力最小，重力也最小．地球表面的重力加速度值由赤道到两极逐渐增大，随距地表高度的增大，重力加速度值在减小．

二、地球上物体的重力和地球对物体的万有引力的关系

　　地球上物体的重力是由于地球的吸引而产生的，它并不等于万有引力．这是因为地球上的物体要随地球自转而做匀速圆周运动，设运动半径 是物体到地轴的距离，所需向心力大小为 ,方向垂直指向地轴，如图所示．物体随地球的自转所需的向心力，是由地球对物体的引力的一个分力提供的，引力的另一个分力才是通常所说的物体受到的重力．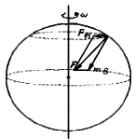

　　地球上物体的重力会随纬度变化而变化．这里的原因有两个：一是由于在不同的纬度上物体随地球自转时的运动半径不同，因而所需的向心力有所不同；另一个是由于地球并不是一个理想的球体，从精确的测量可知，地球是一个极半径比赤道半径略小的椭球体，因而物体位于不同纬度上，地球对它的引力也就有所不同．所以随着纬度的增加，地球对物体的引力逐渐增大，物体随地球自转所需向心力逐渐减小，物体的重力逐渐增大．

　　实际上，由于地球的自转很慢，物体随地球的自转所需的向心力，最大也不过是地球对它的引力的千分之几；而且地球的极半径与赤道半径相差极小，物体的重力在两极与赤道相差也不过千分之几，所以在一般情况下，重力和重力加速度随纬度的变化可忽略不计．

太阳系各行星有关参数

万有引力定律在天文学上的应用

　　A．万有引力是天体间的主要作用力，万有引力定律的发现对天文学的发展起到了巨大的推动作用．

　　B．计算中心天体的质量．①观测行星围绕恒星做匀速圆周运动的轨道半径（r）和运转周期（T），则可以根据万有引力为向心力的道理计算出中心天体（恒星）的质量（M）．②根据同样的道理，只要观测某行星的一颗卫星围绕行星做匀速圆周运动的轨道半径和周期，就能测出该中心天体（行星）的质量．

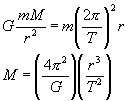
　　C．如果围绕中心天体运动的轨道半径（r）很小、与中心天体自身的半径（R）相差无几，即 ，则可以进一步估算出中心天体的平均密度：

　　D．未知行星——海王星、冥王星的先后被发现，是天文学上应用万有引力定律的成功范例．

应用万有引力定律分析天体（人造卫星）的运动

　　1．基本方法：把天体（或人造卫星）的运动看成是匀速圆周运动，其所需向心力由万有引力提供。

　　公式：

　　解决问题时可根据情况选择公式分析、计算。

　　2．求天体的质量和密度的方法

　　通过观察天体做匀速圆周运动的卫星的周期T、半径r，由万有引力等于向心力得： ,

得天体质量

　　（1）若天体的半径R，则天体的密度

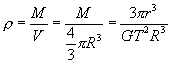
　　（2）若天体的卫星环绕天体表面运动，其轨道半径r等于天体半径R，则天体密度