 设为首页
设为首页
 加入收藏
加入收藏
扩展资料
火车转弯
如图1所示,如果火车转弯处内外轨无高度差,火车行驶到此处时,由于火车惯性的缘故,会造成外轨内侧与火车外轮的轮缘相互挤压现象,使火车受到外轨内侧的侧压力作用.迫使火车转弯做圆周运动.但是这个侧压力的反作用力,作用在外轨上会对外轨产生极大的破坏作用,甚至会引起外轨变形,造成翻车事故.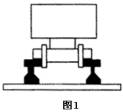
其实火车转弯的向心力并不是侧压力提供的,那么是什么力作为向心力的呢?如图2所示,在转弯处使外轨略高于内轨,火车驶过转弯处时,铁轨对火车的支持力 ![]() 的方向不再是竖直的,而是斜向弯道内侧,它与重力G的合力指向圆心,成为使火车转弯的向心力.
的方向不再是竖直的,而是斜向弯道内侧,它与重力G的合力指向圆心,成为使火车转弯的向心力.
设内外轨间的距离为L,内外轨的高度差为h,火车转弯的半径为R,火车转弯的规定速度为
![]() .由图2所示力的三角形得向心力为:
.由图2所示力的三角形得向心力为: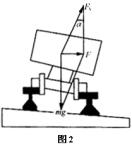
![]()
由牛顿第二定律得:
![]()
所以: ![]()
即火车转弯的规定速度: ![]()
讨论(1)当火车行驶速率v等于规定速度 ![]() 时,
时, ![]() ,内、外轨道对轮缘都没有侧压力.
,内、外轨道对轮缘都没有侧压力.
(2)当火车行驶速度v大于规定速度 ![]() 时,
时, ![]() ,外轨道对轮缘有侧压力.
,外轨道对轮缘有侧压力.
(3)当火车行驶速度v小于规定速度 ![]() 时,
时, ![]() ,内轨道对轮缘有侧压力.
,内轨道对轮缘有侧压力.
扩展资料
竖直面内的圆周运动
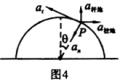
1、如图3所示,是绳子牵引下的小球在竖直面内作圆周运动,如图4所示,是在轨道约束下在竖直面内作圆周运动的小球,它们的共同特点是,在运动到最高点时均没有物体支承小球,下面讨论小球在竖直平面内作圆周运动通过最高点的情况:
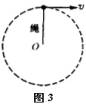
(1)临界条件;绳子和轨道对小球没有力的作用
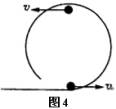
根据牛顿第二定律得 ![]()
即 ![]()
这个速度可理解为恰好转过或恰好转不过的速度.
(2)能过最高点的条件: ![]() (当
(当 ![]() 时绳、轨道对球分别产生拉力、压力)
时绳、轨道对球分别产生拉力、压力)
(3)不能过最高点的条件: ![]() (实际上球还没有到最高点就脱离了轨道)
(实际上球还没有到最高点就脱离了轨道)
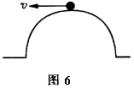
2、如图5所示,是杆子约束下的小球在竖直面内作圆周运动,如图6所示,是在轨道约束下在竖直面内作圆周运动的小球,它们的共同特点是,在运动到最高点时均有物体支承小球,下面讨论小球在竖直平面内作圆周运动通过最高点的情况:
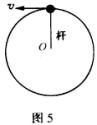
(1)临界条件: ![]() (支承物对物体的支持力等于mg)
(支承物对物体的支持力等于mg)
(2)当 ![]() ,即
,即 ![]() ,如图5所示支承物对物体既没有拉力也没有支持力.
,如图5所示支承物对物体既没有拉力也没有支持力.
当 ![]() ,即
,即 ![]() ,如图5所示支承物对物体产生拉力、且拉力随v增大而增大.如图6所示,小球将脱离轨道作平抛运动,因为轨道不能对它产生拉力.
,如图5所示支承物对物体产生拉力、且拉力随v增大而增大.如图6所示,小球将脱离轨道作平抛运动,因为轨道不能对它产生拉力.
当 ![]() ,即
,即 ![]() ,如图5所示支承物对物体产生支持力,且支持力随v减少而增大,范围是0~mg。
,如图5所示支承物对物体产生支持力,且支持力随v减少而增大,范围是0~mg。
扩展资料
竖直面内圆周运动的临界条件
在竖直平面内的圆周运动,关键是最高点的受力情况的分析.若沿法线方向的合外力满足 ![]() 时,则物体能通过最高点,即能在竖直平面作圆周运动.细绳和轻杆作用下的竖直平面内的圆周运动是常见的,在细绳作用下,小球在最高点的最小合外力是mg.所以,最高点的速度至少为
时,则物体能通过最高点,即能在竖直平面作圆周运动.细绳和轻杆作用下的竖直平面内的圆周运动是常见的,在细绳作用下,小球在最高点的最小合外力是mg.所以,最高点的速度至少为 ![]() .而细杆作用下,既可提供拉力,也可提供支持力,在最高点合外力可以为零,所以通过最高点的速度只需大于零.
.而细杆作用下,既可提供拉力,也可提供支持力,在最高点合外力可以为零,所以通过最高点的速度只需大于零.
扩展资料
通过分析临界状态解决“范围类”题目
如图所示,细绳一端系着质量 ![]() kg的物体,静止于水平面,另一端通过光滑小孔吊着质量
kg的物体,静止于水平面,另一端通过光滑小孔吊着质量 ![]() kg的物体,M的中点与圆孔距离为0.2m,并知M和水平面的最大静摩擦力为2N,现使此平面绕中心轴线转动,问角速度
kg的物体,M的中点与圆孔距离为0.2m,并知M和水平面的最大静摩擦力为2N,现使此平面绕中心轴线转动,问角速度
![]() 在什么范围m会处于静止状态?(
在什么范围m会处于静止状态?( ![]() )
)
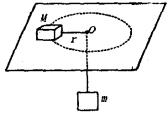
解析:要使m静止,M应与平面相对静止,考虑M能与水平面相对静止的两个极端状态:
当 ![]() 为所求范围的最小值时,M有向圆心运动的趋势,水平面对M的静摩擦力方向背离圆心,大小等于最大静摩擦力2N,此时对M有:
为所求范围的最小值时,M有向圆心运动的趋势,水平面对M的静摩擦力方向背离圆心,大小等于最大静摩擦力2N,此时对M有:
![]() 且
且
![]()
解得: ![]() rad/s.
rad/s.
当 ![]() 为所求范围的最大值时,M有远离圆心运动的趋势,水平面对M的摩擦力方向指向圆心,且大小也为2N,此时:
为所求范围的最大值时,M有远离圆心运动的趋势,水平面对M的摩擦力方向指向圆心,且大小也为2N,此时:
![]() 且
且
![]()
解得: ![]() rad/s
rad/s
故所求 ![]() 的范围为
的范围为 ![]() .
.
说明:分析两个极端(临界)状态来确定变化范围,是求解“范围类”题目的基本思路和方法.
扩展资料
圆周运动中的相对运动问题
解某些复杂的相对运动问题时,会应用到圆周运动的知识.下面举几个小例子.
一、一个半径为R的半圆柱体沿水平方向向右做加速度为a的匀加速运动.在半圆柱体上搁置一根竖直杆,此杆只能沿竖直方向运动(图2).当半圆柱体的速度为v时,杆与半圆柱体接触点P与柱心的连线与竖直方向的夹角为
![]() ,求此时竖直杆运动的速度和加速度.
,求此时竖直杆运动的速度和加速度.
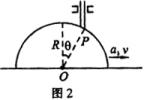
(1)取半圆柱体作为参照系.在此参照系中,P点做圆周运动,即 ![]() 的方向沿着圆上P点的切线方向.根据题意,
的方向沿着圆上P点的切线方向.根据题意, ![]() 的方向是竖直向上的.因为:
的方向是竖直向上的.因为:
![]()
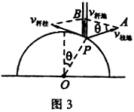
所以可画出矢量三角形PAB(图3),由此可知:
![]()
(2)在半圆柱体参照系中,P点的加速度由切向加速度
![]() 和法向加速度
和法向加速度 ![]() 构成,即:
构成,即:
![]()
其中 ![]()
由相对运动公式,可知
![]() ①
①
①式的矢量图如图4所示。
将①式中的各矢量向 ![]() 方向上投影,可得
方向上投影,可得
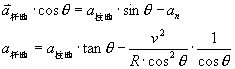
![]()
二、如图5(a)所示,某人以常速率v拉动绳的一端,绳的另一端A系着一只小船,已知人离水面高度为h,试求当绳与水面倾角
![]() 为30°时,小船的速度和加速度。
为30°时,小船的速度和加速度。
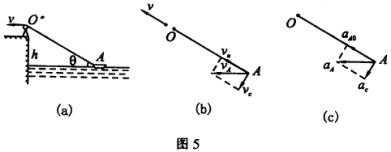
(1)如图(b)所示, ![]() 与
与 ![]() 分别为A点相对于O点的切向速度和法向速度。
分别为A点相对于O点的切向速度和法向速度。
且: ![]()
又因为绳AO不可伸长
有: ![]()
即: ![]()
(2)A点相对O点的加速度可能由两个方面产生。
①绳AO以O点为轴转动,A点相对O点有切向速度,为
![]() ,其相对O点产生一法向加速度
,其相对O点产生一法向加速度 ![]() ,且
,且 ![]() 。
。
②在沿绳方向上,绳相对O点缩短,则A点可能产生一个AO方向的加速度 ![]() 。而本题中,A点在AO方向上相对O点的速度
。而本题中,A点在AO方向上相对O点的速度 ![]() 是一定值,所以
是一定值,所以 ![]() 。A点相对O点的法向加速度:
。A点相对O点的法向加速度:
![]()
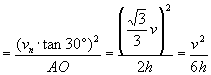
三、有一只狐狸以不变速率
![]() 沿着直线AB逃跑,一只猎犬以不变的速率
沿着直线AB逃跑,一只猎犬以不变的速率 ![]() 追击,其运动方向始终对准狐狸。某时刻狐狸在F处,猎犬在D处,
追击,其运动方向始终对准狐狸。某时刻狐狸在F处,猎犬在D处, ![]() ,且
,且 ![]() (图6),试求此时刻猎犬加速度的大小。
(图6),试求此时刻猎犬加速度的大小。
猎犬做匀速率曲线运动,其加速度的大小和方向都在不断变化。在所求时刻之后的一段很短的时间 ![]() 内,猎犬运动轨迹的曲率半径为
内,猎犬运动轨迹的曲率半径为 ![]() ,则其向心加速度:
,则其向心加速度:
![]()
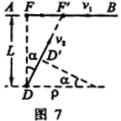
如图7所示,在 ![]() 时间内,狐狸和猎犬分别到达了
时间内,狐狸和猎犬分别到达了 ![]() 和
和 ![]() 处,猎犬的运动方向转过的角度:
处,猎犬的运动方向转过的角度:
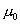
因为 ![]() 很小,所以狐狸运动的距离:
很小,所以狐狸运动的距离:
![]()
因此: ![]()
![]()
所以: ![]()