第三节 平抛物体的运动

扩展资料

根据运动的独立性原理来解斜抛运动

　　根据运动的独立性，经常把斜抛运动分解成水平方向的匀速直线运动和竖直方向的上抛运动来处理，但有时也可以用其它的分解方法．

　　如图所示，从A点以 的初速度抛出一个小球，在离A点水平距离为s处有一堵高度为h的墙BC，要求小球能超过B点．问小球以怎样的角度抛出，才能使 最小？

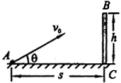
　　先用最一般的坐标取法：以A点作为原点，水平方向（AC方向）作为x轴，竖直方向作为y轴．小球的运动方程为

              

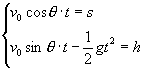
　　可解得                              ①

　　这是一个有关 和 的函数关系，需要求 为多少时 有极小值．将①式改写成

　　即                           ②

　　这是一个有关 的一元二次方程，其判别式为

    ②式的解为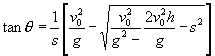

  当 太小时， ,②式无解，说明在此情况下小球不可能越过BC墙，当 时，②式有解，此时的 便是小球能越过墙顶的最小的 ．（因为如果再大，便会有两个 值都能经过墙顶）．

取 作为未知数，可以解得

舍去不合理解，

此时 

这种解法的数学要求较高．

换一种坐标取法：以AB方向作为x轴（如图）．这样一取，小球在x、y方向上做的都是匀变速运动了， 和g都要正交分解到x、y方向上去．

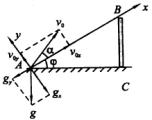
小球的运动方程为

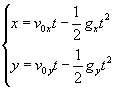
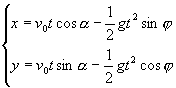
当小球越过墙顶时，y方向的位移为零，由上式可得

                        

则：

  

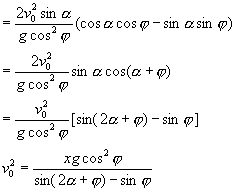
当 最大，即 时， 有极小值．



　　  

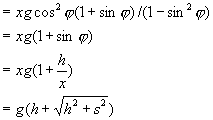
　　比较两种解法的 ，可知两种解法的结果是相同的．第二种解法对数学的要求略低一些，而且求极值的意义也明确一些．

再换一种观念：将斜抛运动看成是 方向的匀速直线运动和另一个自由落体运动的合运动，如图所示．

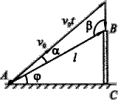
在位移三角形ADB中用正弦定理

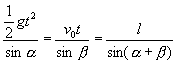                 ①

　　由①式中第一个等式可得              ②

　　将②式代入①式中第二个等式

     

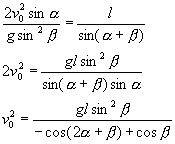
　　当 有极大值1时，即 时， 有极小值．

　　因为          

　　所以           

　　与第二种解法结果相同，很明显，这种解法最简单明了．

　　从这个一题多解中可说明：一个较复杂的运动可按不同的观念分解成不同的两个运动，分得合理会给解题带来一些方便．