第六节 力的分解

力的分解

　　如果几个力产生的效果跟原来的一个力产生的效果相同，这几个力就叫做原来那个力的分力．求一个已知力的分力叫力的分解，力的分解是力的合成的逆运算，遵循平行四边形定则，也就是1221011已知对角线求两个邻边的问题．显然，如果没有附加条件，则可有无数个答案．所以，力的分解关键在于根据具体情况确定某一已知力的实际作用效果．以下两种情况可以得到确定的分力．第一，根据力的实际效果能够确定两个分力的方向，则可得到两个分力的大小；第二，根据力的实际效果能够确定一个分力的方向和大小，则可得到另一个分力的方向和大小．

　　如在图所示的支架悬挂一个重力为 的灯．支架的重力不计．已知 、 、 的长分别为 、 、 ，求支架两杆所受的力．

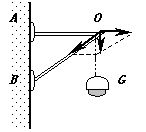
　　解：在支架的 端悬挂电灯后，使支架的两根杆受到力的作用．由于支架的 、 两端与墙壁是绞链连结，因此作用在杆上的力是沿杆的方向．但杆受的是拉力还是压力，需要通过实践来判断．可以设想，若将杆 换成弹簧，则弹簧会被拉长，表示此杆受的是拉力．若将杆 换成弹簧，则弹簧会被压缩，说明此杆受的是压力．这就是灯对支架 端拉力的两个分力所产生的实际效果．判断出两个分力的方向，那么根据平行四边形定则很容易得出杆 受到沿杆向外的拉力:

　　杆 受到沿杆向内的压力

　　在力的分解中，若已知合力的大小、方向和另一分力的方向，则其解要进行讨论．

　　如图所示，一个大人沿与河岸成θ角的方向拉纤，要使平行河岸的船行方向上得到一个合力 ，则另一岸的一个小孩如何用力最小．

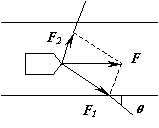
　　这道题已知合力 的大小方向和另一分力 的方向，要求另一分力 最小，由作图法可知有唯一解； 垂直 时， 最小． 

分力与分量

　　在求解动力学问题时，为了能根据研究对象的运动特征，利用牛顿第二定律列出相应的运动方程，往往需要把研究对象所受的诸力按正交分解法进行分解．于是，引入了“力的分量”概念，下文简称分量．但有些参考书又常把“力的分量”称为“分力”．这样，自然就使不少同学把应有区别的“分量”与“分力”这两个概念混为一谈．下面就这两个概念的区别和联系作一些讨论．

　　设有一平面力F，作用在A点，则力F的正交分解如图所示．

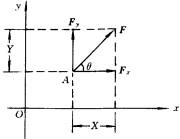
　　（1）图中 、 分别是力F的两个分力．既然都是力，那么它们都具备力的“三要素”，都是矢量．显然，它们的作用点都是原力F的作用点A．图中X、Y分别是力F在x轴和y轴上的“投影”，称为力F在x轴和y轴上的分量．因为投影是个代数量，有正、负之分，故作为力F的分量X、Y也是代数量而不是矢量．

　　（2）从图可知，力F的两个分力 、 的大小与力F在相应坐标轴上的分量绝对值相等，即 ．

　　（3）从图可知，力F的两个分量分别可按下式计算：

　　分量X、Y的正、负号完全由 值的大小决定．

　　当 时， ；

　　当 时， ；

　　当 时， ；

　　当 时， ．

　　可见，力F的分力 、 的方向跟其在x轴和y轴上的两个分量的正、负号紧密联系着．分量为正，则表示分力方向与相应坐标轴的正方向一致；分量为负，则表示分力方向与相应坐标轴的负方向一致．

　　（4）如力F沿两个不正交的坐标轴分解，分力的大小就与分量的绝对值不等．如图所示，力F在x袖和y轴上的分力是 和 ，而相应的分量是X和Y．

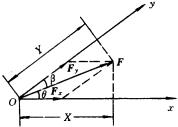
　　显然， ，

力的分解应根据实际产生的效果进行

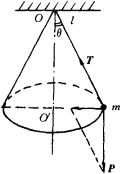
    有这样一个问题：用绳子悬挂着的物体，在水平面内作匀速圆周运动，问绳的张力有多大？

解答有两种不同的结果．一种是：

另一种是：

　　前者认为物体在重力方向上是平衡的，所以该方向上的合力等于零；后者则认为物体在悬绳方向上是平衡的，所以该方向的合力也等于零．哪一种解答是正确的？怎样去分析呢？

　　首先分析物体的运动状态，因为物体是在水平面内作匀速圆周运动，所以它有一个向着中心 的加速度，产生此加速度的力（向心力）显然只能是T和P的合力．从图上不难看出合力的大小等于 ，由此，可得到 的结果．

　　其次从力的分解方面去考虑，一般来说，求已知力的两个分力问题，如果没有附加条件，解答是不定的．在所讨论的圆锥摆中，重力P是已知的，求P的两个分力可有两种分解法：

　　一种是把重力P分解为沿悬线方向和垂直重力方向的两个分力如图；另一种是把重力分解为沿悬线方向和垂直悬线方向的两个分力如图．

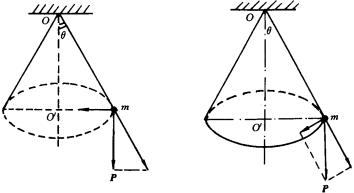
　　哪一种分解法符合实际呢？这就要从重力P产生的实际效果去分析了．题目明确指出，物体在水平面内作匀速圆周运动，那么重力P就只能产生两种效果：使悬线张紧和使物体在水平面内作变加速运动，因而前一种分解是符合实际的．由此也可得到 的正确结果．而第二种分解法，实际上是把圆锥摆的问题误解为单摆的问题了，这是经常容易混淆的问题．