 设为首页
设为首页
 加入收藏
加入收藏
例1.已知地球的半径为![]() ,球面上
,球面上![]() 两点都在北纬45°圈上,它们的球面距离为
两点都在北纬45°圈上,它们的球面距离为![]() ,
,![]() 点在东经30°上,求
点在东经30°上,求![]() 点的位置及
点的位置及![]() 两点所在其纬线圈上所对应的劣弧的长度.
两点所在其纬线圈上所对应的劣弧的长度.
 分析:求点
分析:求点![]() 的位置,如图就是求
的位置,如图就是求![]() 的大小,只需求出弦
的大小,只需求出弦![]() 的长度.对于
的长度.对于![]() 应把它放在
应把它放在![]() 中求解,根据球面距离概念计算即可.
中求解,根据球面距离概念计算即可.
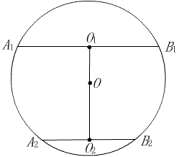
解:如图,设球心为![]() ,北纬45°圈的中心为
,北纬45°圈的中心为![]() ,
,
由![]() 两点的球面距离为
两点的球面距离为![]() ,所以
,所以![]() =
=![]() ,
,
![]()
![]() 为等边三角形.于是
为等边三角形.于是![]() .
.
由![]() ,
,
![]() .即
.即![]() =
=![]() .
.
又![]() 点在东经30°上,故
点在东经30°上,故![]() 的位置在东经120°,北纬45°或者西经60°,北纬45°.
的位置在东经120°,北纬45°或者西经60°,北纬45°.
![]() 两点在其纬线圈上所对应的劣弧
两点在其纬线圈上所对应的劣弧![]() .
.
说明:此题主要目的在于明确经度和纬度概念,及利用球的截面的性质和圆的有关性质设计计算方案.
 例2.用两个平行平面去截半径为
例2.用两个平行平面去截半径为![]() 的球面,两个截面圆的半径为
的球面,两个截面圆的半径为![]() ,
,![]() .两截面间的距离为
.两截面间的距离为![]() ,求球的表面积.
,求球的表面积.
分析:此类题目的求解是首先做出截面图,再根据条件和截面性质做出与球的半径有关的三角形等图形,利用方程思想计算可得.
解:设垂直于截面的大圆面交两截面圆于![]() ,上述大圆的垂直于
,上述大圆的垂直于![]() 的直径交
的直径交![]() 于
于![]() ,如图.
,如图.
设![]() ,则
,则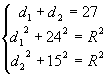 ,解得
,解得![]() .
.
![]() .
.
说明:通过此类题目,明确球的有关计算问题需先将立体问题转化为平面问题,进一步熟悉有关圆的基础知识,熟练使用方程思想,合理设元,列式,求解.
例3.自半径为![]() 的球面上一点
的球面上一点![]() ,引球的三条两两垂直的弦
,引球的三条两两垂直的弦![]() ,求
,求![]() 的值.
的值.
分析:此题欲计算所求值,应首先把它们放在一个封闭的图形内进行计算,所以应引导学生构造熟悉的几何体并与球有密切的关系,便于将球的条件与之相联.
解:以![]() 为从一个顶点出发的三条棱,将三棱锥
为从一个顶点出发的三条棱,将三棱锥![]() 补成一个长方体,则另外四个顶点必在球面上,故长方体是球的内接长方体,则长方体的对角线长是球的直径.
补成一个长方体,则另外四个顶点必在球面上,故长方体是球的内接长方体,则长方体的对角线长是球的直径.
![]()
![]() =
=![]() .
.
说明:此题突出构造法的使用,以及渗透利用分割补形的方法解决立体几何中体积计算.
例4.试比较等体积的球与正方体的表面积的大小.
分析:首先抓好球与正方体的基本量半径和棱长,找出等量关系,再转化为其面积的大小关系.
解:设球的半径为![]() ,正方体的棱长为
,正方体的棱长为![]() ,它们的体积均为
,它们的体积均为![]() ,
,
则由![]() ,
,![]() ,由
,由![]() 得
得![]() .
.
![]() .
.
![]() .
.
![]()
![]()
![]() ,即
,即![]() .
.
说明:突出相关的面积与体积公式的准确使用,注意比较大小时运算上的设计.
例5.如图1所示,在棱长为1的正方体内有两个球相外切且又分别与正方体内切.(1)求两球半径之和;(2)球的半径为多少时,两球体积之和最小.
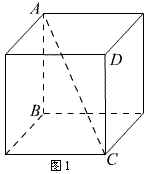
分析:此题的关键在于作截面,一个球在正方体内,学生一般知道作对角面,而两个球的球心连线也应在正方体的体对角线上,故仍需作正方体的对角面,得如图2的截面图,在图2中,观察![]() 与
与![]() 和棱长间的关系即可.
和棱长间的关系即可.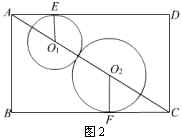
解:如图2,球心![]() 和
和![]() 在
在![]() 上,过
上,过![]() ,
,![]() 分别作
分别作![]() 的垂线交于
的垂线交于![]() .
.
则由![]() 得
得![]() .
.
![]() ,
,
![]() .
.
(1)设两球体积之和为![]() ,
,
则![]()
=![]()
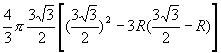
=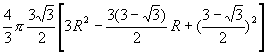
当![]() 时,
时,![]() 有最小值.
有最小值.![]() 当
当![]() 时,体积之和有最小值.
时,体积之和有最小值.
例6.设正四面体中,第一个球是它的内切球,第二个球是它的外接球,求这两个球的表面积之比及体积之比.
分析:此题求解的第一个关键是搞清两个球的半径与正四面体的关系,第二个关键是两个球的半径之间的关系,依靠体积分割的方法来解决的.
解:如图,正四面体![]() 的中心为
的中心为![]() ,
,![]() 的中心为
的中心为![]() ,则第一个球半径为正四面体的中心到各面的距离,第二个球的半径为正四面体中心到顶点的距离.
,则第一个球半径为正四面体的中心到各面的距离,第二个球的半径为正四面体中心到顶点的距离.
 设
设![]() ,正四面体的一个面的面积为
,正四面体的一个面的面积为![]() .
.
依题意得![]() ,
,
又![]()
![]() 即
即![]() .
.
所以![]() .
.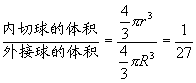 .
.
点评:正四面体与球的接切问题,可通过线面关系证出,内切球和外接球的两个球心是重合的,为正四面体高的四等分点,即定有内切球的半径![]() (
(![]() 为正四面体的高),且外接球的半径
为正四面体的高),且外接球的半径![]() .
.
*例7.把四个半径都是1的球中的三个放在桌面上,使它两两外切,然后在它们上面放上第四个球,使它与前三个都相切,求第四个球的最高点与桌面的距离.
分析:关键在于能根据要求构造出相应的几何体,由于四个球半径相等,故四个球一定组成正四面体的四个顶点且正四面体的棱长为两球半径之和2.
解:由题意,四球心组成棱长为2的正四面体的四个顶点,
则正四面体的高![]() .
.
而第四个球的最高点到第四个球的球心距离为求的半径1,且三个球心到桌面的距离都为1,故第四个球的最高点与桌面的距离为![]() .
.
说明:此类型题目对培养学生空间想象能力,并根据题意构造熟悉几何体都非常有帮助,且还可以适当增加一点实际背景,加强应用意识.