第八节 棱锥

典型例题（例1～例3）

　　例1 正六棱锥的底面周长为24，侧面与底面所成角为 ，求：（1）棱锥的高；（2）斜高；（3）侧棱长；（4）侧棱与底面所成角．

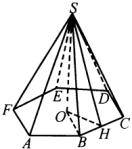
　　分析：本题涉及了正棱锥的若干基本量，可以把基本量放置到直角三角形中，由已知量求未知量．

　　解：正六棱锥的底面周长为24．

　　∴正六棱锥的底面边长为4．

　　在正棱锥 中，

　　取 中点 ，连 ， ，

　　 是正六边形 的中心．

　　连 ，则 底面

　　∴ ．

　　∴ 是侧面与底面所成二面角的平面角，即 ．

　　（1）在 △ 中， ， ，

　　∴ ．

　　（2）同样在△ 中，斜高 ，

　　（3） △ 中， ， ．

　　∴ ．

　　（4）∵ 底面 ，∴ 是侧棱与底面所成角，

　　同样在△ 中， ，∴ ，

　　说明：在立体几何中，要善于把长度和角度放到三角形中去解决，正棱锥中有关长度、角度主要在两上重要的直角三角形中，本题中的方法也可用于其它正棱锥中．比如：已知正四棱锥底面边长为 ，相邻两侧面所成二面角为 ，求正棱锥的高、斜高、侧棱长．正四棱锥相邻侧面是全等的等腰三角形，利用这个性质先落实相邻侧面所成二面的平面角，先计算侧棱长为 ，然后利用底面边长和侧棱长在两个重要的直角三角形中，计算出高为 ，斜高为 ．

　　例2 如图所示，正四棱锥 棱长均为13， ， 分别是 ， 上的点，且 ．

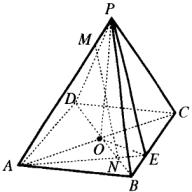　　 （1）求证：直线 平面 ；

　　（2）求直线 与底面 所成角的正弦．

　　分析：（1）要证明 平面 ，只需证明 与平面 内某一条直线平行．为此连 并延长交 于 ，连 ．可考虑证明 ．（2）若能证明 ，则 即为直线 与底面所成的角．

　　解：（1）连 并延长交 于 ，再连 ．

　　∵ ，∴ ，

　　又 ，

　　∴ ，

　　∴ ，

　　又 平面 ， 平面 ，∴ 平面 ．

　　（2）设 为底面中心，连 ， ，则 平面 ．又 ，则 为直线 与平面 所成的角．

　　由 及 ，得 ，在△ 中， ， ， ，由余弦定理，得 ．在 △ 中， ， ，则 ．

　　说明：本题（2）若直接求 与平面 所成的角，计算就比较复杂，而平移为求 与底面所成的角，计算就易得多．可见，平移是求线线、线面所成角的重要方法．

　　例3 斜三棱柱 的底面△ 是直角三角形， ，侧棱与底面成 角，点 在底面的射影 为 的中点， ．

　　（1）求证 ；

　　（2）若 为 的二面角，求四棱锥 的体积．

　　分析：证 关键在于证出其中一条线垂直于另一条线所在的平面；而求棱锥的体积关键在于求出其底面积和高．这两个问题可由题设及线与线、线与面的位置关系求得．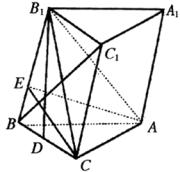

　　解：如图所示，

　　（1）∵ 平面 ， 底面 ，

　　∴ ．

　　∵ ，

　　∴ 平面 ，∴ ．

　　∵ 在底面 上的射影 为 的中点，侧棱与底面成 角，

　　∴四边形 是菱形，∴ ，

　　∴ 平面 ，∴ ．

　　（2）过 作 ，连结 ．

　　∵ 平面 ，

　　∴ 是 在平面 上的射影，

　　∴ ，

　　∴ 是二面角 的平面角，

　　∴ ．

　　在 △ 中， ，在 △ 中，由 可得 ．

　　∴ ，

　　∴

　　　　　　

　　　　　　

　　　　　　 

　　　　　　

　　　　　　 ．

　　∴  （体积单位）．

　　说明：证明线线垂直转化成证线面垂直是证明时常用的方法之一，而证线面垂直时又涉及线与线的垂直，因此线与面各种位置关系经常贯穿问题的始终．当遇到一线垂直于一截面，而截面面积又能计算时，将几何体分割成两个体积之和计算也是一种常用的方法．结果便转化成截面与此线相乘的关系，因而使问题得到简化．

典型例题（例4～例6）

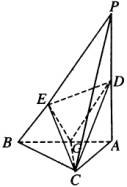　　例4　如图，在三棱锥 中， 底面 ， ， 、 分别是 和 的中点， 为 上一点，且 ， ．

　　（1）求证： 平面 ；

　　（2）求截面 分棱锥 所成两部分的体积之比．

　　分析：由 底面 ，可以判定平面 平面 ，且相交于 ，因为 是 的中点，且 ，所以 ，于是有 平面 ， ．

　　若证 平面 ，只需 与平面 中的另一条直线垂直就可以了．为此，就要从已知的数量关系着手，找到新的线与线的垂直关系．

　　平面 把三棱锥 分成两部分，显然这两部分具有相同的高线 ．所以，只要找到△ 和四边形 的面积之比，就可以确定两部分的体积之比了．

　　证明：（1）∵ 平面 ，且 平面

　　∴平面 平面 ，且相交于

　　在△ 中，∵ ， 是 边上的中线

　　∴ ．∴ 平面

　　∵ 平面 ，∴

　　利用两个平面垂直的性质定理可以证明 平面

　　在 △ 和△ 中

　　设 ，则 ， ， ，

　　∵ ，

　　∵ ，∴△ ～△

　　∵ ，∴

　　∴ ．∵

　　利用相似三角形的性质，得到

　　∴

　　∵ ，∴ 平面 ．

　　解：（2）∵

　　

　　∵ ，

　　∴

　　∴

　　∴

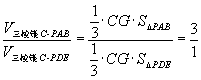
　　∴截面 分棱锥 为两部分，三棱锥 与四棱锥 的体积之比为1：2．

　　 例5  四棱锥 ，侧面 是边长为2的正三角形且与底面垂直，底面 是面积为 的菱形， 为菱形的锐角．（1）求证： ；（2）求二面角 的大小；（3）求棱锥 的侧面积与体积．

　　分析：取 中点 ，侧面 底面 ，从而 可利用三垂线定理转化为证明 ，线面垂直也为二面角 平面角的落实创造了有利条件，棱锥的侧面积可通过抓侧面三角形的特殊性来解决．

　　证明：（1）取 中点 ，连 、 ，

　　∵△ 是等边三角形，∴ ，

　　∵面 底面 ，∴ 底面 ，

　　∵等边△ 的边长为2，∴

　　∴菱形 的边长为2，又菱形的面积是 ，

　　∴ ，∴ ，又 是锐角，

　　∴ ，∴△ 是等边三角形，

　　∴ ， 在平面 上射影为 ，∴ ．

　　解：（2）∵ ，由（1） ， ，

　　∴ ， ．

　　∴ 是二面角 的平面角，

　　在 △ 中 ，

　　∴ ，即二面角 的大小为 ．

　　（3）由（2）在 △ 中，可得 ，

　　在 △ 中， ， ，

　　∴ ， ，

　　在△ 中， ， ，可得 ，

　　在△ 中， ， ，可得 ，

　　又正△ 边长为2，∴ ，

　　∴ ，

　　∵ ，∴ ．

　　说明：抓线面垂直关系是解决立体几何问题的关键，非特殊棱柱、棱锥的侧面积，往往要通过逐个计算每个侧面的面积相加而得到，这就需要分析每个侧面的具体特点，比如是否为矩形、直角三角形、等边三角形等．可以举一个类似的例子，四棱锥 的高为1，底面为菱形，侧面 和侧面 所成角为 ，且都垂直于底面，另两侧面与底面都成 角，求棱锥的全面积．这里由相交平面 与 都与底面垂直得到 垂直于底面，利用 底面 ，一方面落实了棱锥的高为 ，另一方面几个二面角的平面角都能方便地落实，四个侧面中，有两个是等腰三角形，有两个是直角三角形，通过计算可得，全面积为 ．

　　例6 已知三棱锥 中， 、 、 与底面 所成角相等， ， ， 为 中点， 点在 上且 截面 ，（1）求 与底面 所成角；（2）求 到平面 的距离．

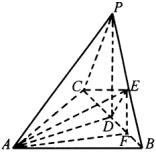　　 分析：由 、 、 与底面所成角相等可得 点在面 上射影为△ 的外心，由于△ 是直角三角形，可以得到 面 ， 面 可转化为 ， 是 中点，找出 到面 的垂线落实 与面 所成角． 到面 的距离可从两方面得到，一方面直接找 到面 的垂线，另一方面，用等积法可求点到面的距离．

　　解：（1）∵ 、 、 与底面 成相等的角，设 在面 上射影为 ，则有 ，

　　∴△ ≌△ ≌△ ，

　　∴ 且 ，

　　∴ 是△ 的外心．

　　∵△ 是直角三角形，且 是斜边 的中点，

　　∴ 点和 点重合，即 面 ，

　　∵ 截面 ，过 的平面 与平面 交于 ，

　　∴ ，∵ 是 中点，∴ 是 中点，

　　取 中点 ，则 ，∴ 平面 ，

　　∴ 为 与底面 所成角．

　　∵ ，∴ ，

　　∵ 且 ，∴ ．

　　又 ，∴△ 也是等腰直角三角形，

　　∴ ，∴ ，

　　在 △ 中， ，

　　∴ ，即 与平面 所成角为 ．

　　（2）方法一：∵ 平面 ，∴ ．

　　又∵ ，∴ 平面 ，∴ ．

　　由（1）△ 是直角三角形， ，∴ ，

　　∵ ，∴ ，∴ 平面 ．

　　∵ ，∴ ．

　　即 到平面 的距离为 ．

　　方法二：∵ ， ，∴ 平面 ，

　　∴ ，又 ， ．

　　∴ ，

　　∵ ， ，

　　设 到面 的距离为 ，

　　∴ ，∴ ．

　　 ，即 到平面 的距离为 ．