 设为首页
设为首页
 加入收藏
加入收藏
例1.根据叙述作图,指出二面角的平面角并证明.
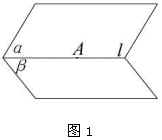
(1)如图1,已知 ![]() .在
.在 ![]() 内作
内作 ![]() 于
于 ![]() ,在
,在 ![]() 内作
内作 ![]() 于
于 ![]() .
.
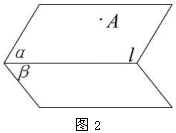
(2)如图2,已知 ![]() .作
.作 ![]() 于
于 ![]() ,在
,在 ![]() 内作
内作 ![]() 于
于 ![]() ,连结
,连结 ![]() .
.
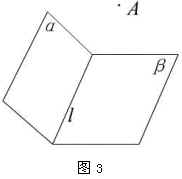
(3)已知 ![]() .作
.作 ![]() 于
于 ![]() ,
, ![]() 于
于 ![]() ,
, ![]() 平面
平面 ![]() ,连结
,连结 ![]() 、
、 ![]() .
.
作图与证明在此省略.
说明:本题介绍了作二面角的平面角的三种常用方法,其中用三垂线定理及逆定理的方法最常用,还需补充这种方法的其他典型图形.
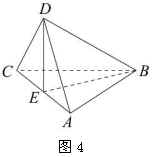
例2. 如图4,在立体图形 ![]() 中,若
中,若 ![]() 是
是 ![]() 的中点,则下列命题中正确的是(
).
的中点,则下列命题中正确的是(
).
(A)平面 ![]() ⊥平面
⊥平面 ![]()
(B)平面 ![]() ⊥平面
⊥平面 ![]()
(C)平面 ![]() ⊥平面
⊥平面 ![]() ,且平面
,且平面 ![]() ⊥平面
⊥平面 ![]()
(D)平面 ![]() ⊥平面
⊥平面 ![]() ,且平面
,且平面 ![]() ⊥平面
⊥平面 ![]()
分析:要判断两个平面的垂直关系,就需固定其中一个平面,找另一个平面内的一条直线与第一个平面垂直.
解:因为 ![]() 且
且 ![]() 是
是 ![]() 的中点,所以
的中点,所以 ![]() 同理有
同理有 ![]() ,于是
,于是 ![]() 平面
平面 ![]() .因为
.因为 ![]() 平面
平面 ![]() ,所以平面
,所以平面 ![]()
![]() 平面
平面 ![]() .又由于
.又由于 ![]() 平面
平面 ![]() ,所以平面
,所以平面 ![]()
![]() 平面
平面 ![]() .所以选C.
.所以选C.
说明:本题意图是训练学生观察图形,发现低级位置关系以便得到高级位置关系.在某一个平面内,得到线线垂直的重要途径是出现等腰三角形底边的中线,由线线垂直得到线面垂直,由线面垂直可得到面面垂直.
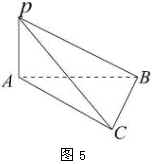
例3.如图5, ![]() 是
是 ![]() 所在平面外的一点,且
所在平面外的一点,且 ![]() 平面
平面 ![]() ,平面
,平面 ![]() 平面
平面 ![]() .求证
.求证 ![]() .
.
分析:已知条件是线面垂直和面面垂直,要证明两条直线垂直,应将两条直线中的一条纳入一个平面中,使另一条直线与该平面垂直,即从线面垂直得到线线垂直..
证明:在平面 ![]() 内作
内作 ![]() ,交
,交 ![]() 于
于 ![]() .因为平面
.因为平面 ![]() 平面
平面 ![]() 于
于 ![]() ,
, ![]() 平面
平面 ![]() ,且
,且 ![]() ,所以
,所以 ![]() .又因为
.又因为 ![]() 平面
平面 ![]() ,于是有
,于是有 ![]() ①.另外
①.另外 ![]() 平面
平面 ![]() ,
, ![]() 平面
平面 ![]() ,所以
,所以 ![]() .由①②及
.由①②及 ![]() ,可知
,可知 ![]() 平面
平面 ![]() .因为
.因为 ![]() 平面
平面 ![]() ,所以
,所以 ![]() .
.
说明:在空间图形中,高一级的垂直关系中蕴含着低一级的垂直关系,通过本题可以看到,面面垂直
![]() 线面垂直
线面垂直 ![]() 线线垂直.
线线垂直.
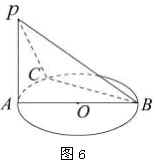
例4.如图6, ![]() 是⊙
是⊙ ![]() 的直径,
的直径, ![]() 垂直于⊙
垂直于⊙ ![]() 所在的平面,
所在的平面, ![]() 是圆周上异于
是圆周上异于 ![]() 、
、 ![]() 的任意一点,求证:平面
的任意一点,求证:平面 ![]()
![]() 平面
平面 ![]() .
.
分析:证明面面垂直的有两个依据,一是证明二面角的平面角为直角,二是利用两个平面垂直的判定定理.由于
![]() 点的任意性,用方法一的可能性不大,所以要寻求线面垂直.
点的任意性,用方法一的可能性不大,所以要寻求线面垂直.
证明:因为 ![]() 是⊙
是⊙ ![]() 的直径,
的直径, ![]() 是圆周上的点,所以有
是圆周上的点,所以有 ![]() ①.
①.
因为 ![]() 平面
平面 ![]() ,
, ![]() 平面
平面 ![]() ,则
,则 ![]() ②.
②.
由①②及 ![]() ,得
,得 ![]() 平面
平面 ![]() .
.
因为 ![]() 平面
平面 ![]() ,有平面
,有平面 ![]()
![]() 平面
平面 ![]() .
.
说明:与上例相逆,低一级的垂直关系是判定高一级垂直关系的依据,根据条件,由线线垂直
![]() 线面垂直
线面垂直 ![]() 面面垂直.通过以上两个例题展示了空间直线与平面的位置关系的内在联系,垂直关系的判定和性质共同构成了一个完整的知识体系.
面面垂直.通过以上两个例题展示了空间直线与平面的位置关系的内在联系,垂直关系的判定和性质共同构成了一个完整的知识体系.
例5.如图7,点 ![]() 在锐二面角
在锐二面角 ![]() 的棱
的棱 ![]() 上,在面
上,在面 ![]() 内引射线
内引射线 ![]() ,使
,使 ![]() 与
与 ![]() 所成的角
所成的角 ![]() 为
为 ![]() ,与面
,与面 ![]() 所成的角大小为
所成的角大小为 ![]() ,求二面角
,求二面角 ![]() 的大小。
的大小。
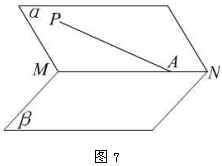
分析:首先根据条件作出二面角的平面角,然后将平面角放入一个可解的三角形中(最好是直角三角形),通过解三角形使问题得解.
解:在射线 ![]() 上取一点
上取一点 ![]() ,作
,作 ![]() 于
于 ![]() ,连结
,连结 ![]() ,则
,则 ![]() 为射线
为射线 ![]() 与平面
与平面 ![]() 所成的角,
所成的角, ![]() .再作
.再作 ![]() ,交
,交 ![]() 于
于 ![]() ,连结
,连结 ![]() ,则
,则 ![]() 为
为 ![]() 在平面
在平面 ![]() 内的射影.由三垂线定理的逆定理,
内的射影.由三垂线定理的逆定理, ![]() ,
, ![]() 为二面角
为二面角 ![]() 的平面角.
的平面角.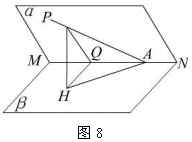 设
设 ![]() ,在
,在 ![]() 中,
中, ![]() ,
,
在 ![]() △
△ ![]() 中,
中,![]()
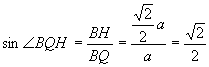 ,
,
![]() 是锐角,
是锐角, ![]() ,即二面角
,即二面角 ![]() 等于
等于 ![]() .
.
说明:本题综合性较强,在一个图形中出现了两条直线所称的角,斜线与平面所称的角,二面角等空间角,这些空间角都要转化为平面角,而且还要彼此联系相互依存,要根据各个平面角的定义添加适当的辅助线.
例6.如图9,将边长为 ![]() 的正三角形
的正三角形 ![]() 以它的高
以它的高 ![]() 为折痕折成一个二面角
为折痕折成一个二面角 ![]() .
.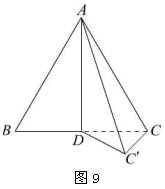
(1)指出这个二面角的面、棱、平面角;
(2)若二面角 ![]() 是直二面角,求
是直二面角,求 ![]() 的长;
的长;
(3)求 ![]() 与平面
与平面 ![]() 所成的角;
所成的角;
(4)若二面角 ![]() 的平面角为
的平面角为 ![]() ,求二面角
,求二面角 ![]() 的平面角的正切值.
的平面角的正切值.
分析:根据问题及图形依次解决.
解:(1)![]() 二面角
二面角 ![]() 的面为
的面为 ![]() 和面
和面 ![]() ,棱为
,棱为 ![]() ,二面角的平面角为
,二面角的平面角为 ![]() .
.
(2)若 ![]() ,
, ![]() .
.
(3)![]() 平面
平面 ![]() ,
, ![]() 为
为 ![]() 与平面
与平面 ![]() 所成的角.在直角三角形
所成的角.在直角三角形 ![]() 中,
中, ![]() ,于是
,于是 ![]() .
.
(4)取 ![]() 的中点
的中点 ![]() ,连结
,连结 ![]() 、
、 ![]() ,
,
![]() ,
,
![]() 为二面角
为二面角 ![]() 的平面角.
的平面角.
![]()
在直角三角形 ![]() 中,
中, ![]()
![]()
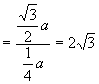 .
.
说明:这是一个折叠问题,要不断地将折叠前后的图形加以比较,抓住折叠前后的变与不变量.