 设为首页
设为首页
 加入收藏
加入收藏
例1 若 ![]() ,
, ![]() ,则
,则 ![]() ,
, ![]() 的位置关系是( )
的位置关系是( )
A.异面直线 B.相交直线
C.平行直线 D.相交直线或异面直线
分析 判断两条直线的位置关系,可以通过观察满足已知条件的模型或图形而得出正确结论.
解:如图所示,在正方体 ![]() 中,设
中,设 ![]() ,
, ![]() ,则
,则 ![]() .
.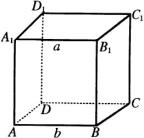
若设 ![]() ,则
,则 ![]() 与
与 ![]() 相交.若设
相交.若设 ![]() ,则
,则 ![]() 与
与 ![]() 异面.
异面.
故选D.
说明:利用具体模型或图形解决问题的方法既直观又易于理解.一般以正方体、四面体等为具体模型.例如, ![]() ,
, ![]() 相交,
相交, ![]() ,
, ![]() 相交,则
相交,则 ![]() ,
, ![]() 的位置关系是相交、平行或异面.类似地;
的位置关系是相交、平行或异面.类似地; ![]() ,
, ![]() 异面,
异面, ![]() ,
, ![]() 异面,则
异面,则 ![]() ,
, ![]() 的位置关系是平行、相交或异面.这些都可以用正方体模型来判断.
的位置关系是平行、相交或异面.这些都可以用正方体模型来判断.
例2 已知直线 ![]() 和点
和点 ![]() ,
, ![]() ,求证:过点
,求证:过点 ![]() 有且只有一条直线和
有且只有一条直线和 ![]() 平行.
平行.
分析:“有且只有”的含义表明既有又惟一,因而这里要证明的有两个方面,即存在性和惟一性.
存在性,即证明满足条件的对象是存在的,它常用构造法(即找到满足条件的对象来证明);惟一性,即证明满足条件的对象只有一个,换句话说,说是不存在第二个满足条件的对象.
因此,这是否定性命题,常用反证法.
证明:(1)存在性.
∵![]() ,∴
,∴ ![]() 和
和 ![]() 可确定一个平面
可确定一个平面 ![]() ,
,
由平面几何知识知,在 ![]() 内存在着过点
内存在着过点 ![]() 和
和 ![]() 平行的直线.
平行的直线.
(2)惟一性
假设在空间过点 ![]() 有两条直线
有两条直线 ![]() 和
和 ![]() 满足
满足 ![]() 和
和 ![]() .根据公理4,必有
.根据公理4,必有 ![]() 与
与 ![]() 矛盾,
矛盾,
∴ 过点 ![]() 有一条且只有一条直线和
有一条且只有一条直线和 ![]() 平行.
平行.
说明:对于证明“有且只有”这类问题,一定要注意证明它的存在性和惟一性.
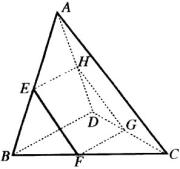 例3 如图所示,设
例3 如图所示,设 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别是空间四边表
分别是空间四边表 ![]() 的边
的边 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 上的点,且
上的点,且 ![]() ,
, ![]() ,求证:
,求证:
(1)当 ![]() 时,四边形
时,四边形 ![]() 是平行四边形;
是平行四边形;
(2)当 ![]() 时,四边形
时,四边形 ![]() 是梯形.
是梯形.
分析:只需利用空间等角定理证明 ![]() 即可.
即可.
证明:连结 ![]() ,
,
在 ![]() 中,
中, ![]() ,∴
,∴ ![]() ,且
,且 ![]() .
.
在 ![]() 中,
中, ![]() ,∴
,∴ ![]() ,且
,且 ![]() .
.
∴ ![]() ,
,
∴ 顶点 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 在由
在由 ![]() 和
和 ![]() 确定的平面内.
确定的平面内.
(1)当 ![]() 时,
时, ![]() ,故四边形
,故四边形 ![]() 为平行四边形;
为平行四边形;
(2)当 ![]() 时,
时, ![]() ,故四边形
,故四边形 ![]() 是梯形.
是梯形.
说明:显然,课本第11页的例题就是本题(2)的特殊情况.
特别地,当 ![]() 时,
时, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 是空间四边形各边中点,以它们为顶点的四边形是平行四边形.
是空间四边形各边中点,以它们为顶点的四边形是平行四边形.
如果再加上条件 ![]() ,这时,平行四边形
,这时,平行四边形 ![]() 是菱形.
是菱形.
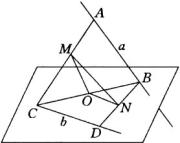 例4 已知
例4 已知 ![]() 是两条异面直线,直线
是两条异面直线,直线 ![]() 上的两点
上的两点 ![]() 的距离为6,直线
的距离为6,直线 ![]() 上的两点
上的两点 ![]() 的距离为8,
的距离为8, ![]() 的中点分别为
的中点分别为 ![]() 且
且 ![]() ,求异面直线
,求异面直线 ![]() 所成的角.
所成的角.
分析:解题的关键在于依据异面直线所成角的定义构造成和异面直线 ![]() 平行的两条相交直线,然后把它们归纳到某一三角形中求解.
平行的两条相交直线,然后把它们归纳到某一三角形中求解.
解:如图,连结 ![]() ,并取
,并取 ![]() 的中点
的中点 ![]() ,连结
,连结 ![]() ,
,
∵ ![]() 分别是
分别是 ![]() 和
和 ![]() 的中位线,
的中位线,
∴ ![]() ,
, ![]() ,即
,即
![]() ,
, ![]() .
.
∴ ![]() 所成的锐角或直角是异面直线
所成的锐角或直角是异面直线 ![]() 所成的角.
所成的角.
又∵ ![]() ,
, ![]() ,
,
∴ ![]() ,
, ![]() .
.
在 ![]() 中,又∵
中,又∵ ![]() ,
,
∴ ![]() ,
,
∴ ![]() .
.
故异面直线 ![]() 所成的角是
所成的角是 ![]() .
.
评注:在求两条异面直线所成的角时,一般要依据已知条件,找出与两条异面直线分别平行并且相交于一点的两条直线.但是,异面直线所成角的定义中的点 ![]() 一般是在图形中存在着的,需要认真观察分析图形的性质,从而找出这一点和过这一点与两异面直线平行的直线,以得到两条异面直线所成的角,在求这个角的大小时,一般是根据平面图形中解三角形的知识求解的.
一般是在图形中存在着的,需要认真观察分析图形的性质,从而找出这一点和过这一点与两异面直线平行的直线,以得到两条异面直线所成的角,在求这个角的大小时,一般是根据平面图形中解三角形的知识求解的.
例5 已知四面体 ![]() 的所有棱长均为
的所有棱长均为 ![]() .求:
.求:
(1)异面直线 ![]() 的公垂线段
的公垂线段 ![]() 及
及 ![]() 的长;
的长;
(2)异面直线 ![]() 和
和 ![]() 所成的角.
所成的角.
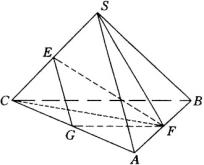 分析:依异面直线的公垂线的概念求作异面直线
分析:依异面直线的公垂线的概念求作异面直线
![]() 的公垂线段,进而求出其距离;对于异面直线所成的角可采取平移构造法求解.
的公垂线段,进而求出其距离;对于异面直线所成的角可采取平移构造法求解.
解:(1)如图,分别取 ![]() 的中点
的中点 ![]() ,连结
,连结 ![]() .
.
由已知,得 ![]() ≌
≌ ![]() .
.
∴ ![]() ,
, ![]() 是
是 ![]() 的中点,
的中点,
∴ ![]() .
.
同理可证 ![]()
∴ ![]() 是
是 ![]() 的公垂线段.
的公垂线段.
在 ![]() 中,
中, ![]() ,
, ![]() .
.
∴ ![]()
![]() .
.
(2)取 ![]() 的中点
的中点 ![]() ,连结
,连结 ![]() ,则
,则 ![]() .
.
∴ ![]() 和
和 ![]() 所成的锐角或直角就是异面直线
所成的锐角或直角就是异面直线 ![]() 和
和 ![]() 所成的角.
所成的角.
连结 ![]() ,在
,在 ![]() 中,
中, ![]() ,
, ![]() ,
, ![]() .
.
由余弦定理,得
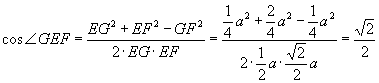 .
.
∴ ![]() .
.
故异面直线 ![]() 和
和 ![]() 所成的角为
所成的角为 ![]() .
.
评注:对于立体几何问题要注意转化为平面问题来解决,同时要将转化过程简要地写出来,然后再求值.