第三节 双曲线及其标准方程

典型例题（例1～例3）

　　例1　讨论 表示何种圆锥曲线，它们有何共同特征．

　　分析：由于 ， ，则 的取值范围为 ， ， ，分别进行讨论．

　　解：（1）当 时， ， ，所给方程表示椭圆，此时 ， ， ，这些椭圆有共同的焦点（－4，0），（4，0）．

　　（2）当 时， ， ，所给方程表示双曲线，此时， ， ， ，这些双曲线也有共同的焦点（－4，0），）（4，0）．

　　（3） ， ， 时，所给方程没有轨迹．

　　说明：将具有共同焦点的一系列圆锥曲线，称为同焦点圆锥曲线系，不妨取一些 值，画出其图形，体会一下几何图形所带给人们的美感．

　　例2　根据下列条件，求双曲线的标准方程．

　　（1）过点 ， 且焦点在坐标轴上．

　　（2） ，经过点（－5，2），焦点在 轴上．

　　（3）与双曲线 有相同焦点，且经过点

　　解：（1）设双曲线方程为 ,∵ 、 两点在双曲线上，

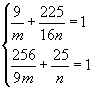　　∴ 解得

　　∴所求双曲线方程为

　　说明：采取以上“巧设”可以避免分两种情况讨论，得“巧求”的目的．

　　（2）∵焦点在 轴上， ，

　　∴设所求双曲线方程为： （其中 ）

　　∵双曲线经过点（－5，2），∴

　　∴ 或 （舍去）

　　∴所求双曲线方程是

　　说明：以上简单易行的方法给我们以明快、简捷的感觉．

　　（3）设所求双曲线方程为：

　　∵双曲线过点 ，∴

　　∴ 或 （舍）

　　∴所求双曲线方程为

　　说明：（1）注意到了与双曲线 有公共焦点的双曲线系方程为 后，便有了以上巧妙的设法．

　　（2）寻找一种简捷的方法，须有牢固的基础和一定的变通能力，这也是在我们教学中应该注重的一个重要方面．

　　例3　已知双曲线 的右焦点分别为 、 ，点 在双曲线上的左支上且 ，求 的大小．

　　分析：一般地，求一个角的大小，通常要解这个角所在的三角形．

　　解：∵点 在双曲线的左支上

　　∴

　　∴

　　∴

　　∵

　　∴

　　说明：（1）巧妙地将双曲线的定义应用于解题当中，使问题得以简单化．

　　（2）题目的“点 在双曲线的左支上”这个条件非常关键，应引起我们的重视，若将这一条件改为“点 在双曲线上”结论如何改变呢？请读者试探索．

典型例题（例4～例7）

　　例4　已知 、 是双曲线 的两个焦点，点 在双曲线上且满足 ，求 的面积．

　　分析：利用双曲线的定义及 中的勾股定理可求 的面积．

　　解：∵ 为双曲线 上的一个点且 、 为焦点．

　　∴ ,

　　∵

　　∴在 中，

　　∵

　　∴

　　∴

　　∴

　　说明：双曲线定义的应用在解题中起了关键性的作用．

　　2．利用双曲线定义求动点的轨迹

　　例5　已知两点 、 ，求与它们的距离差的绝对值是6的点的轨迹．

　　分析：问题的条件符合双曲线的定义，可利用双曲线定义直接求出动点轨迹．

　　解：根据双曲线定义，可知所求点的轨迹是双曲线．

　　∵ ，

　　∴

　　∴所求方程 为动点的轨迹方程，且轨迹是双曲线．

　　说明：（1）若清楚了轨迹类型，则用定义直接求出其轨迹方程可避免用坐标法所带来的繁琐运算．

　　（2）如遇到动点到两个定点距离之差的问题，一般可采用定义去解．

　　例6　在 中， ，且 ，求点 的轨迹．

　　分析：要求点 的轨迹，需借助其轨迹方程，这就要涉及建立坐标系问题，如何建系呢？

　　解：以 所在直线为 轴，线段 的中垂线为 轴建立平面直角坐标系，则 ， ．

　　设 ，由 及正弦定理可得：

　　∵

　　∴点 在以 、 为焦点的双曲线右支上设双曲线方程为：

　　∴ ， ,∴ ， ,∴

　　∴所求双曲线方程为

　　∵ ,∴

　　∴点 的轨迹是双曲线的一支上挖去了顶点的部分

　　例7　求下列动圆圆心 的轨迹方程：

　　（1）与⊙ 内切，且过点

　　（2）与⊙ 和⊙ 都外切．

　　（3）与⊙ 外切，且与⊙ 内切．

　　分析：这是圆与圆相切的问题，解题时要抓住关键点，即圆心与切点和关键线段，即半径与圆心距离．如果相切的⊙ 、⊙ 的半径为 、 且 ，则当它们外切时， ；当它们内切时， ．解题中要注意灵活运用双曲线的定义求出轨迹方程．

　　解：设动圆 的半径为

　　（1）∵⊙ 与⊙ 内切，点 在⊙ 外

　　∴ ， ，

　　∴点 的轨迹是以 、 为焦点的双曲线的左支，且有：

， ，

　　∴双曲线方程为

　　（2）∵⊙ 与⊙ 、⊙ 都外切

　　∴ ， ，



　　∴点 的轨迹是以 、 为焦点的双曲线的上支，且有：

， ，

　　∴所求的双曲线的方程为：

　　（3）∵⊙ 与⊙ 外切，且与⊙ 内切

　　∴ ， ，

　　∴点 的轨迹是以 、 为焦点的双曲线的右支，且有：

， ，

　　∴所求双曲线方程为：

　　说明：（1）“定义法”求动点轨迹是解析几何中解决点轨迹问题常用而重要的方法．

　　（2）巧妙地应用“定义法”可使运算量大大减小，提高了解题的速度与质量．

　　（3）通过以上题目的分析，我们体会到了，灵活准确地选择适当的方法解决问题是我们无休止的追求目标．