第六节 曲线和方程

典型例题

　　例1：如果命题“坐标满足方程 的点都在曲线 上”不正确，那么以下正确的命题是

　　（A）曲线 上的点的坐标都满足方程 ．

　　（B）坐标满足方程 的点有些在 上，有些不在 上．

　　（C）坐标满足方程 的点都不在曲线 上．

　　（D）一定有不在曲线 上的点，其坐标满足方程 ．

　　分析：举例，若方程为 ，曲线为第一、三象限角平分线，易知答案为D．

　　例2：求到两条垂直相交直线的距离之和等于定值的点的轨迹方程，并指出图形的形状．

　　解：以两条垂直相交直线为坐标轴，建立直角坐标系．设点 ，由点 分别向两条坐标轴作垂线，垂足分别为 、 ，依题意，可得  （ 为常数）

　　进而式　　

　　当 ， 时， ；

　　当 ， 时， ；

　　当 ， 时， ；

　　当 ， 时， ；

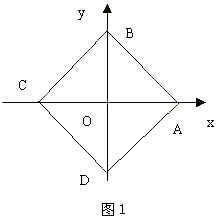
　　图形是以 ， ， ， 为顶点的正方形，如图１所示．

　　例3：已知一条曲线上的每一点到点 的距离都是它到点 的距离的一半，求这条曲线的方程．

　　解：设 是曲线上任意一点，则

　　代入坐标有

　　化简得曲线方程为

．

　　例4：已知两定点 、 ，一动点 与 、 连线的夹角为 ，求动点 的轨迹方程．

　　解：设 ，由夹角公式有

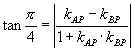
　　即

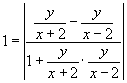
　　化简得

　　（1）当 时， ；

　　（2）当 时， ．

　　例5：过 点作两条互相垂直的直线 ， ，若 交 轴于 ， 交 轴于 ，求线段 中点 的轨迹方程．

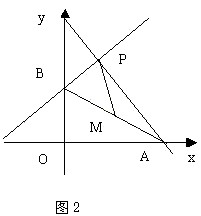　　解：连接 ，设 ，则 ， ．

　　∵  

　　∴   为直角三角形．

　　由直角三角形性质知

　　即

　　化简得 的轨迹方程为

　　说明：本题也可以用勾股定理求解，还可以用斜率关系求解，因此本题可有三种解法．用斜率求解的过程要麻烦一些．

返回页首