 设为首页
设为首页
 加入收藏
加入收藏
例1 画出不等式组 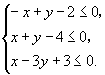 表示的平面区域.
表示的平面区域.
分析 采用“图解法”确定不等式组每一不等式所表示的平面区域,然后求其公共部分.
解 把 ![]() ,
, ![]() 代入
代入 ![]() 中得
中得 ![]()
∴ 不等式 ![]() 表示直线
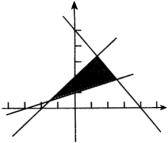
表示直线 ![]() 下方的区域(包括边界),即位于原点的一侧,同理可画出其他两部分,不等式组所表示的区域如图所示.
下方的区域(包括边界),即位于原点的一侧,同理可画出其他两部分,不等式组所表示的区域如图所示.
说明 “图解法”是判别二元一次不等式所表示的区域行之有效的一种方法.
例2 若 ![]() 、
、 ![]() 满足条件
满足条件 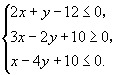 求
求 ![]() 的最大值和最小值.
的最大值和最小值.
分析 画出可行域,平移直线找最优解.
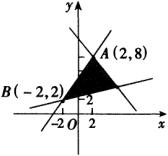
解 作出约束条件所表示的平面区域,即可行域,如图所示.
作直线 ![]() ,即
,即 ![]() ,它表示斜率为
,它表示斜率为 ![]() ,纵截距为
,纵截距为 ![]() 的平行直线系,当它在可行域内滑动时,由图可知,直线
的平行直线系,当它在可行域内滑动时,由图可知,直线 ![]() 过点时,
过点时, ![]() 取得最大值,当
取得最大值,当 ![]() 过点
过点 ![]() 时,
时, ![]() 取得最小值.
取得最小值.
∴ ![]() ∴
∴ ![]()
说明 解决线性规划问题,首先应明确可行域,再将线性目标函数作平移取得最值.
例3 某糖果厂生产 ![]() 、
、 ![]() 两种糖果,
两种糖果, ![]() 种糖果每箱获利润40元,
种糖果每箱获利润40元, ![]() 种糖果每箱获利润50元,其生产过程分为混合、烹调、包装三道工序,下表为每箱糖果生产过程中所需平均时间(单位:分钟)
种糖果每箱获利润50元,其生产过程分为混合、烹调、包装三道工序,下表为每箱糖果生产过程中所需平均时间(单位:分钟)
| 混合 |
烹调 |
包装 |
|
|
|
1 |
5 |
3 |
|
|
2 |
4 |
1 |
每种糖果的生产过程中,混合的设备至多能用12机器小时,烹调的设备至多只能用机器30机器小时,包装的设备只能用机器15机器小时,试用每种糖果各生产多少箱可获得最大利润.
分析 找约束条件,建立目标函数.
解 设生产 ![]() 种糖果
种糖果 ![]() 箱,
箱, ![]() 种糖果
种糖果 ![]() 箱,可获得利润
箱,可获得利润 ![]() 元,则此问题的数学模式在约束条件
元,则此问题的数学模式在约束条件 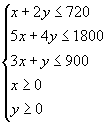 下,求目标函数
下,求目标函数 ![]() 的最大值,作出可行域,其边界
的最大值,作出可行域,其边界![]()
![]()
![]()
![]()
![]()
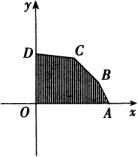 由
由 ![]() 得
得 ![]() ,它表示斜率为
,它表示斜率为 ![]() ,截距为
,截距为 ![]() 的平行直线系,
的平行直线系, ![]() 越大,
越大, ![]() 越大,从而可知过
越大,从而可知过 ![]() 点时截距最大,
点时截距最大, ![]() 取得了最大值.
取得了最大值.
解方程组 ![]()
∴ ![]() 即生产
即生产 ![]() 种糖果120箱,生产
种糖果120箱,生产 ![]() 种糖果300箱,可得最大利润19800元.
种糖果300箱,可得最大利润19800元.
说明 由于生产 ![]() 种糖果120箱,生产
种糖果120箱,生产 ![]() 种糖果300箱,就使得两种糖果共计使用的混合时间为120+2×300=720(分),烹调时间5×120+4×300=1800(分),包装时间3×120+300=660(分),这说明该计划已完全利用了混合设备与烹调设备的可用时间,但对包装设备却有240分钟的包装时间未加利用,这种“过剩”问题构成了该问题的“松驰”部分,有待于改进研究.
种糖果300箱,就使得两种糖果共计使用的混合时间为120+2×300=720(分),烹调时间5×120+4×300=1800(分),包装时间3×120+300=660(分),这说明该计划已完全利用了混合设备与烹调设备的可用时间,但对包装设备却有240分钟的包装时间未加利用,这种“过剩”问题构成了该问题的“松驰”部分,有待于改进研究.
例4 甲、乙、丙三种食物的维生素 ![]() 、
、 ![]() 含量及成本如下表:
含量及成本如下表:
| 甲 |
乙 |
丙 |
|
| 维生素 |
600 |
700 |
400 |
| 维生素 |
800 |
400 |
500 |
| 成本(元/千克) |
11 |
9 |
4 |
某食物营养研究所想用 ![]() 千克甲种食物,
千克甲种食物, ![]() 千克乙种食物,
千克乙种食物, ![]() 千克丙种食物配成100千克的混合食物,并使混合食物至少含56000单位维生素
千克丙种食物配成100千克的混合食物,并使混合食物至少含56000单位维生素 ![]() 和63000单位维生素
和63000单位维生素 ![]() .(1)用
.(1)用 ![]() 、
、 ![]() 表示混合物成本
表示混合物成本 ![]() .(2)确定
.(2)确定 ![]() 、
、 ![]() 、
、 ![]() 的值,使成本最低.
的值,使成本最低.
分析 找到线性约束条件及目标函数,用平行线移动法求最优解.
解 (1)依题意: ![]() 、
、 ![]() 、
、 ![]() 满足
满足 ![]()
∴ 成本 ![]() (元)
(元)
(2)依题意 ![]()
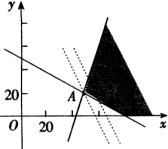 ∵
∵
![]()
∴ 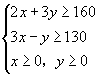
作出不等式组所对应的可行域,如图所示.
联立 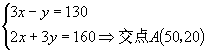
作直线 ![]() 则易知该直线截距越小,
则易知该直线截距越小, ![]() 越小,所以该直线过
越小,所以该直线过 ![]() 时,直线在
时,直线在 ![]() 轴截距最小,从而
轴截距最小,从而 ![]() 最小,此时7×50+5×20+400=
最小,此时7×50+5×20+400=![]() =850元
=850元
∴ ![]() 千克,
千克, ![]() 千克时成本最低.
千克时成本最低.